Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении $2:1$, считая от вершины.

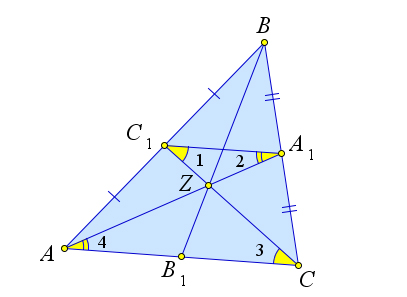
Рассмотрим треугольник $ABC$, в котором проведены медианы $AA_1, BB_1$ и $CC_1$.

Докажем, что все медианы пересекаются в одной точке.
Пусть медианы $AA_1$ и $CC_1$ пересекаются в точке $Z$.

Заметим, что $A_1C_1$ – средняя линия треугольника $ABC$.

Следовательно, $A_1C_1\parallel AC$, и $\angle 1=\angle 3, \angle 2=\angle 4$, и, следовательно $\triangle A_1C_1Z\sim \triangle ACZ$.

Тогда $\dfrac{A_1C_1}{AC}=\dfrac{1}{2}=\dfrac{C_1Z}{CZ}=\dfrac{A_1Z}{AZ}$.

Аналогично, если рассмотреть медианы $BB_1$ и $AA_1$, то они пересекаются в точке, разбивающей медиану $AA_1$ в таком же отношении $1:2$, считая от точки $A_1$, а это точка $Z$.

Итак, все медианы пересекаются в точке $Z$ и делятся ею в отношении $2:1$, считая от вершины треугольника.

Рассмотрим треугольник $ABC$, в котором проведены медианы $AA_1, BB_1$ и $CC_1$.

Докажем, что все медианы пересекаются в одной точке.

Действительно, так как $\dfrac{AC_1}{C_1B}\cdot\dfrac{BA_1}{A_1C}\cdot\dfrac{CB_1}{B_1A}=1$, то по теореме Чевы медианы пересекаются в одной точке. Обозначим эту точку $Z$.

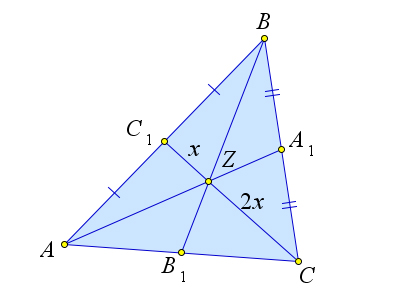
По теореме Менелая для треугольника $ABB_1$ и секущей $CC_1$ имеем $\dfrac{AC_1}{C_1B}\cdot\dfrac{BZ}{ZB_1}\cdot\dfrac{B_1C}{CA}=1$, откуда $\dfrac{BZ}{ZB_1}=\dfrac{2}{1}$.

Аналогично $\dfrac{AZ}{ZA_1}=\dfrac{CZ}{ZC_1}=\dfrac{2}{1}$.

Медианы делят треугольник на шесть равных по площади треугольников.

Рассмотрим треугольник $ABC$, в котором проведены медианы $AA_1, BB_1$ и $CC_1$.

Пусть они пересекаются в точке $Z$.

Докажем, что шесть образовавшихся треугольников равны по площади.

Найдем площадь треугольника $AC_1Z$.

Треугольники $AC_1C$ и $CC_1B$ имеют общую высоту, проведенную из вершины $C$, а поскольку их основания равны, то и площади равны: $S_{CC_1B}=S_{AC_1C}=\frac{1}{2}\cdot S_{ABC}$.

Треугольники $ACZ$ и $AZC_1$ имеют общую высоту, проведенную из вершины $A$, следовательно, их площади относятся, как основания: $S_{ACZ}:S_{AC_1Z}=CZ:ZC_1=2:1$.

Тогда $S_{AC_1Z}=\dfrac{1}{3}\cdot S_{ACC_1}=\dfrac{1}{3}\cdot\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{6} S_{ABC}$.

Аналогично можно найти площади других получившихся треугольников, и они будут тоже равны $\dfrac{1}{6}\cdot S_{ABC}$.