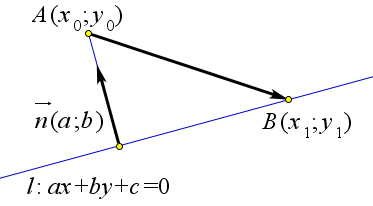
Расстояние от точки $A(x_0;y_0)$ до прямой $l:\ ax+by+c=0$ выражается по формуле $\rho(A;l)=\dfrac{|ax_0+b_0+c|}{\sqrt{a^2+b^2}}$.

Рассмотрим произвольную точку $B(x_1;y_1)$ прямой $l$.

Вектор $\vec{n}(a;b)$ является нормалью к прямой $l$.

Тогда $\rho(A;l)=\mbox{Пр}_{\vec{n}}(\overrightarrow{AB})$.

По пункту $3$ теоремы $\ref{151}$ $pr_{\vec{n}}(\overrightarrow{AB})=\frac{|\vec{n}\cdot \overrightarrow{AB}|}{|\vec{n}|}=\frac{|(x_1-x_0;y_1-y_0)\cdot(a;b)|}{\sqrt{a^2+b^2}}=\frac{|x_1a-x_0a+y_1b-y_0b|}{\sqrt{a^2+b^2}}=\frac{|-x_0a-y_0b+x_1a+y_1b|}{\sqrt{a^2+b^2}}$.

Так как точка $B(x_1;y_1)$ лежит на прямой $l$, то $ax_1+by_1+c=0$, то есть $ax_1+by_1=-c$.

Подставив это выражение в последнее равенство, получим: $\rho(A;l)=\frac{|-ax_0-by_0-c|}{\sqrt{a^2+b^2}}=\frac{|+ax_0+by_0+c|}{\sqrt{a^2+b^2}}$.

Модуль в числителе необходим, чтобы выражение было положительным вне зависимости от выбора направления нормали к прямой.