Если $m_c$ – медиана треугольника, проведенная к стороне $c$, то $m_c=\frac{1}{2}\sqrt{2a^2+2b^2-c^2}$, где $a$ и $b$ – остальные стороны треугольника.

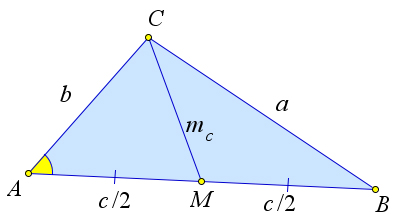
Рассмотрим треугольник $ABC$ со сторонами $a,b,c$ и медианой $CM=m_c$.

Докажем, что $m_c=\dfrac{1}{2}\sqrt{2a^2+2b^2-c^2}$.

По теореме косинусов для треугольника $ABC$ имеем: $\cos{A}=\dfrac{b^2+c^2-a^2}{2bc}$.

По теореме косинусов для треугольника $ACM$ имеем: $m_c^2=b^2+\left(\dfrac{c}{2}\right)^2-2b\dfrac{c}{2}\cos{A}=b^2+\dfrac{c^2}{4}-\dfrac{b^2+c^2-a^2}{2}=\dfrac{4b^2+c^2-2b^2-2c^2+2a^2}{4}=\dfrac{2a^2+2b^2-c^2}{4}$.

Откуда после извлечения корня из обеих частей равенства и следует, что $m_c=\dfrac{1}{2}\sqrt{2a^2+2b^2-c^2}$.

Если $m_c$ – медиана треугольника, проведенная к стороне $c$, то $m_c=\frac{1}{2}\sqrt{a^2+b^2+2ab\cos{\gamma}}$, где $a$ и $b$ – остальные стороны треугольника.