Теорема
- Площадь треугольника равна половине произведения двух его сторон на синус угла, заключенного между ними.
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла, заключенного между ними.
- Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Доказательство
Докажем первый пункт теоремы.
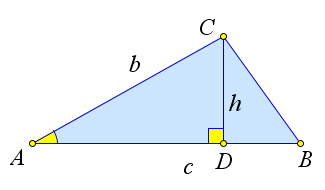
Пусть в треугольнике $ABC$ известны стороны $b, c$ и угол $A$ между ними.
Докажем, что $S_{ABC}=\dfrac{1}{2}bc\sin{A}$.
Действительно, проведем высоту $h=CD$ из вершины $C$.
Тогда $\sin{A}=\frac{h}{b}$.
Поэтому $h=b\sin{A}$.
Тогда $S_{ABC}=\dfrac{1}{2}ch=\dfrac{1}{2}bc\sin{A}$.
Докажем второй пункт теоремы.
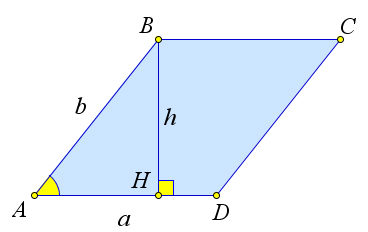
Пусть в параллелограмме $ABCD$ известны стороны $a, b$ и угол $A$ между ними.
Докажем, что $S_{ABCD}=ab\sin{A}$.
Действительно, проведем высоту $h=BH$ из вершины $B$.
Тогда $\sin{A}=\frac{h}{b}$.
Поэтому $h=b\sin{A}$.
Тогда $S_{ABCD}=ah=ab\sin{A}$.
Докажем третий пункт теоремы.
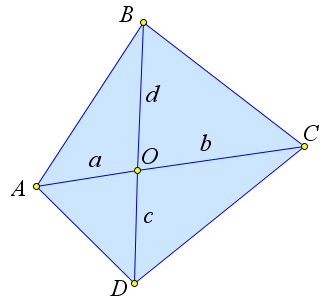
Рассмотрим произвольный выпуклый четырехугольник.
Пусть его диагонали пересекаются в точке $O$.
Обозначим $a=AO, b=CO, c=DO, d=BO$.
Кроме того, $\angle AOB=\angle COD$, а углы $\angle BOC$ и $\angle AOD$ являются смежными к ним.
Следовательно, синусы углов $\angle AOB, \angle BOC, \angle COD$ и $\angle AOD$ равны.
Обозначим $\sin{\angle AOB}=\sin{\alpha}$.
Тогда $S_{ABCD}=S_{ABO}+S_{BOC}+S_{COD}+S_{AOD}=\dfrac{1}{2}\sin{\alpha}(ad+db+bc+ca)=\dfrac{1}{2}\sin{\alpha}(d(a+b)+c(b+a))=\dfrac{1}{2}\sin{\alpha}(a+b)(c+d)=\dfrac{1}{2}\sin{\alpha}\cdot AC\cdot BD$.
Теорема
В любом выпуклом четырехугольнике $ABCD$ выполняется соотношение $S_{AOB}\cdot S_{COD}=S_{BOC}\cdot S_{AOD}$.
Доказательство
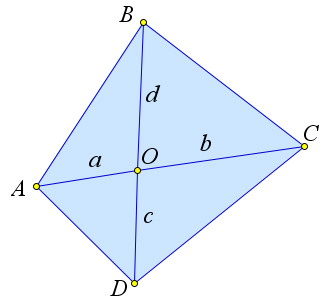
Рассмотрим произвольный выпуклый четырехугольник.
Пусть его диагонали пересекаются в точке $O$.
Обозначим $a=AO, b=CO, c=DO, d=BO$.
Кроме того, $\angle AOB=\angle COD$, а углы $\angle BOC$ и $\angle AOD$ являются смежными к ним.
Следовательно, синусы углов $\angle AOB, \angle BOC, \angle COD$ и $\angle AOD$ равны.
Обозначим $\sin{\angle AOB}=\sin{\alpha}$.
Тогда $S_{ABO}\cdot S_{COD}=\dfrac{1}{2}\sin{\alpha}\cdot ad\cdot\dfrac{1}{2}\sin{\alpha}\cdot bc=\dfrac{1}{2}\sin{\alpha}\cdot db\cdot\dfrac{1}{2}\sin{\alpha}\cdot ac=S_{BOC}\cdot S_{AOD}$.
Следствие
В произвольной трапеции площади треугольников, на которые трапецию делят диагонали, удовлетворяют соотношению $S^2=S_1\cdot S_2$.
Доказательство
Рассмотрим трапецию $ABCD$ в которой диагонали $AC$ и $BD$ пересекаются в точке $O$.
По теореме $S_{AOB}=S_{COD}=S$.
Обозначим $S_1=S_{BOC}$, $S_2=S_{AOD}$.
Тогда, учитывая теорему, получим $S^2=S_1\cdot S_2$.