Парабола

Парабола – это геометрическое место точек, равноудаленных от данной прямой и данной точки, не лежащей на этой прямой. Прямая называется директрисой, а точка – фокусом параболы.

Каноническое уравнение параболы имеет вид $y^2=2px$. При этом уравнение директрисы $x=-\frac{p}{2}$, фокус $F(\frac{p}{2};0)$.

Пусть точка $F(\frac{p}{2};0)$ – это фокус параболы, а прямая $l$ с уравнением $x=-\frac{p}{2}$ – это её директриса.

Пусть точка $M(x;y)$ – это произвольная точка параболы.

Тогда по определению $MF=\rho(M;l)$.

Используя формулу расстояния между двумя точками, получим $\sqrt{(x-\frac{p}{2})^2+y^2}=x+\frac{p}{2}$.

Возведя обе части этого уравнения в квадрат, раскрыв скобки и сократив подобные слагаемые, получим $y^2=2px$.

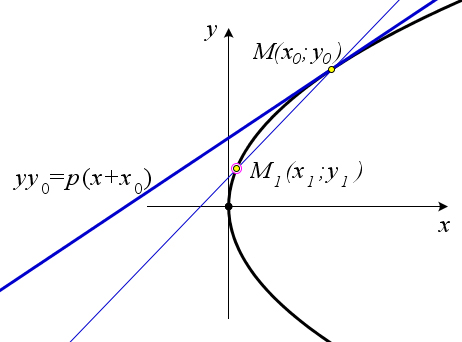
Пусть точка $M_0(x_0;y_0)$ – произвольная точка параболы $y^2=2px$. Тогда уравнение касательной к параболе, проведенной в этой точке имеет вид $yy_0=p(x+x_0)$.

По определению касательной к кривой в данной токе $M$ называется предельное положение секущей $M_0M_1$ при условии, что точка $M_1$ стремится к точке $M_0$ по данной кривой.

Рассмотрим уравнение секущей к параболе, проходящей через точку $M_0(x_0;y_0)$ и не совпадающую с ней точку $M_1(x_1;y_1)$ (рис. \ref{pic154}).

Так как обе точки лежат на параболе $y^2=2px$, то их координаты можно записать в виде $M_0(\frac{y_0^2}{2p};y_0), M_1(\frac{y_1^2}{2p};y_1)$.

Запишем уравнение прямой $M_0M_1$: $\frac{x-x_0}{x_0-x_1}=\frac{y-y_0}{y_0-y_1}, \frac{x-\frac{y_0^2}{2p}}{\frac{y_0^2}{2p}-\frac{y_1^2}{2p}}=\frac{y-y_0}{y_0-y_1}, \frac{2px-y_0^2}{y_0^2-y_1^2}=\frac{y-y_0}{y_0-y_1}, 2px-y_0^2=(y-y_0)(y_0+y_1)$.

Если точка $M_1$ стремиться к точке $M_0$ по параболе, то $y_1$ стремиться к $y_0$.

Тогда последнее равенство можно записать в виде $2px-y_0^2=(y-y_0)\cdot2y_0$ или $2px-y_0^2=2yy_0-2y_0^2, 2px+y_0^2=2yy_0$. А так как $y_0^2=2px_0$, то получаем уравнение $2px+2px_0=2yy_0$ или $p(x+x_0)=yy_0$.

1. Любой луч света, исходящий из фокуса параболы, после отражения от параболы становится параллельным оси параболы.
2. Если источник света помещен в фокусе параболы, то фронт отраженной от параболы волны представляет собой отрезок, соединяющий две точки параболы и параллельный ее директрисе.

Рассмотрим каноническую параболу $y^2=2px$.

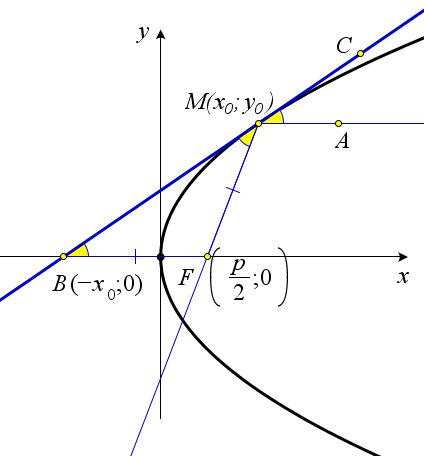
Пусть $F(\frac{p}{2};0)$ – это фокус параболы, а точка $M(x_0;y_0)$ произвольная точка данной параболы.

Пусть луч света $FM$, отразившись от параболы переходит в луч $MA$. Кроме того, пусть $B$ – это точка пересечения оси $Ox$ с касательной к параболе, проведенной в точке $M$.

По свойству отражения луча света $\a BMF=\a CMF$.

Докажем, что треугольник $BMF$ – равнобедренный.

Так как ордината точки $B$ равна нулю, то из уравнения касательной $yy_0=p(x+x_0)$ легко найти, что абсцисса точки $B$ равна $-x_0$.

По формуле расстояния между двумя точками, имеем: $MF=\sqrt{(x_0-\frac{p}{2})^2+y_0}=\sqrt{(x_0-\frac{p}{2})^2+2px_0}=\sqrt{(x_0+\frac{p}{2})^2}=x_0+\frac{p}{2}=BF$.

Таким образом $\angle FBM=\angle FMB$, следовательно, $\angle FBM=\angle CMF$.

А так как эти углы являются соответственными, то прямые $MA$ и $BF$ параллельны.

Докажем второй пункт теоремы.

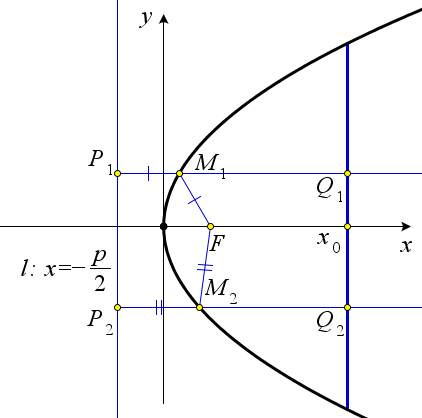
Необходимо доказать, что вне зависимости от выбора точки на параболе сумма расстояний от неё до фокуса и до выбранного фронта будет постоянна.

Пусть фронт волны изображается прямой $x=x_0$.

Докажем, что для точек $M_1$ и $M_2$ будет выполнено $FM_1+M_1Q_1=FM_2+M_2Q_2$.

По первому пункту теоремы лучи $M_1Q_1$ и $M_2Q_2$ параллельны оси параболы, следовательно, они перпендикулярны директрисе.

Тогда по определению параболы $FM_1=M_1P$ и $FM_2=M_2P_2$.

Тогда $FM_1+M_1Q_1=P_1M_1+M_1Q_1=P_1Q_1=x_0+\frac{p}{2}=P_2Q_2=P_2M_2+M_2Q_2=M_2F+M_2Q_2$.