Обобщенная теорема синусов
В треугольнике со сторонами $a,b,c$, углами $\alpha,\beta,\gamma$ и радиусом описанной окружности $R$ выполняется соотношение $2R=\dfrac{a}{\sin{\alpha}}=\dfrac{b}{\sin{\beta}}=\dfrac{c}{\sin{\gamma}}$.
Доказательство
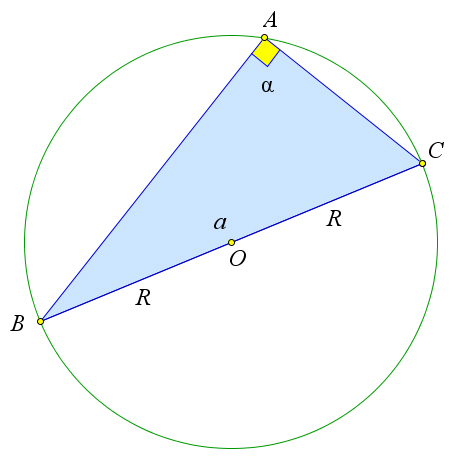
Рассмотрим треугольник $ABC$, около которого описана окружность с центром $O$ и радиусом $R$.
Обозначим $a=BC, \alpha=\angle A$.
Докажем, что $\dfrac{BC}{\sin{\angle A}}=2R$ или $2R=\dfrac{a}{\sin{\alpha}}$.
Возможны три случая: когда угол $\angle \alpha$ прямой, острый или тупой.
Рассмотрим первый случай.
Пусть угол $A$ прямой.
Так как вписанный угол равный $90^\circ$ опирается на диаметр, то $BC=2R$.
Но так как $\sin{A}=\sin{90^\circ}=1$, то $BC=2R\cdot 1=BC\sin{\alpha}$.
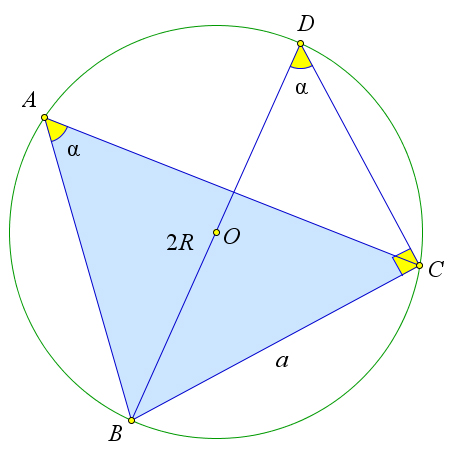
Рассмотрим второй случай.
Пусть угол $\angle A$ – острый.
Проведем диаметр $BD$ и рассмотрим треугольник $\triangle DBC$.
Так как углы $\angle A$ и $\angle D$ опираются на одну и туже дугу $\buildrel\,\,\frown\over{BC}$, то $\angle A=\angle D$.
Кроме того, угол $\angle BCD$ опирается на диаметр, следовательно, $\angle BCD=90^\circ$.
Тогда из прямоугольного треугольника $\triangle BCD$ $\sin{D}=\dfrac{BC}{2R}$ или $2R=\dfrac{BC}{\sin{A}}$.
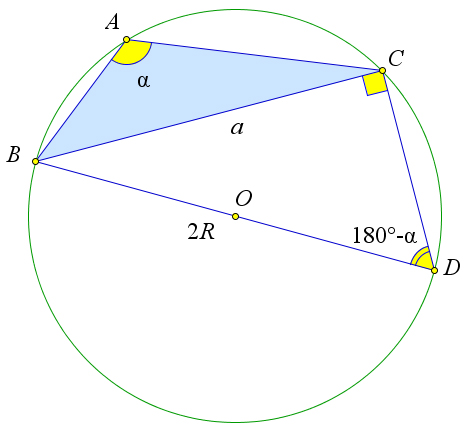
Рассмотрим третий случай.
Пусть угол $\angle A$ – тупой.
Проведем диаметр $BD$ и рассмотрим треугольник $\triangle DBC$.
Так как угол $\angle A$ опирается на дугу $\buildrel\,\,\frown\over{BDC}$, а угол $\angle D$ опирается на дугу $\buildrel\,\,\frown\over{BAC}$, то $\angle D=180^\circ-\angle A$.
Кроме того, угол $\angle BCD$ опирается на диаметр, следовательно, $\angle BCD=90^\circ$.
Тогда из прямоугольного треугольника $\triangle BCD$ получим $\sin{D}=\dfrac{BC}{2R}=\sin{(180^\circ-\angle A)}=\sin{A}$ или $2R=\dfrac{BC}{\sin{A}}$.