Параллелограмм

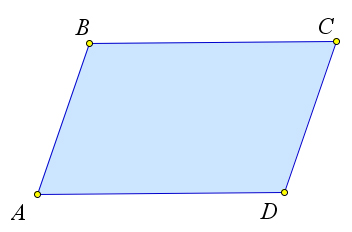
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

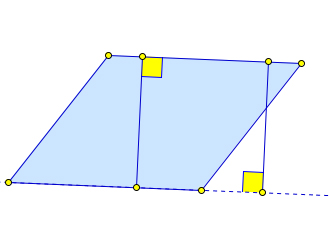
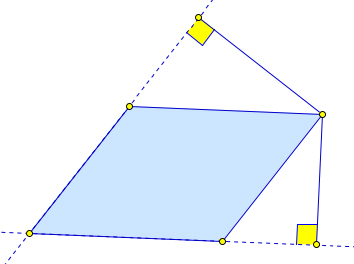
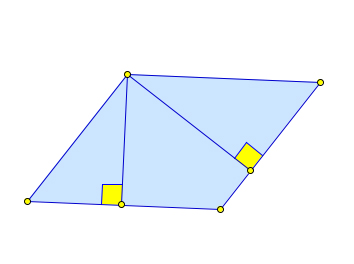
Высотой параллелограмма называется перпендикуляр, опущенный из точки на стороне параллелограмма на прямую, содержащую параллельную ей сторону, а также длина этого перпендикуляра.

Из каждой вершины параллелограмма можно провести две высоты.

• Свойства параллелограмма
• Признаки параллелограмма

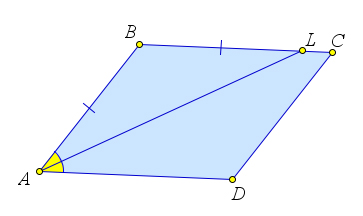
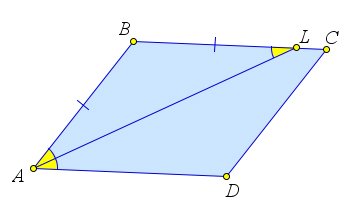
Если в параллелограмме $ABCD$ из угла $A$ проведена биссектриса $AL$ ($L\in(BC)$), то треугольник $ABL$ – равнобедренный.

Так как $BC\parallel AD$, то $\angle LAD=\angle BLA$, как накрест лежащие.

Но тогда $\angle BAL=\angle BLA$, и треугольник $BAL$ – равнобедренный.

Биссектрисы соседних углов параллелограмма пересекаются под прямым углом.

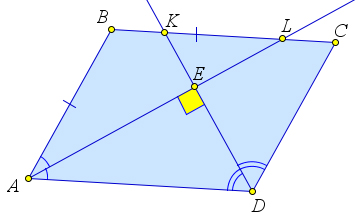
Пусть биссектрисы $AL$ и $DK$ пересекаются в точке $E$.

Рассмотрим треугольник $AED$.

Так как $AL$ и $DK$ - биссектрисы, то $\angle EAD + \angle EDA = \dfrac{1}{2}\left(\angle A + \angle D\right)=\dfrac{1}{2}\cdot 180^\circ=90^\circ$.