Теорема
Доказательство
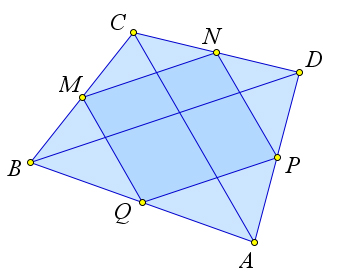
Первый случай
Пусть $MNPQ$ – параллелограмм Вариньона для выпуклого
четырехугольника $ABCD$, и пусть $S_{ABCD}=S$.
Докажем, что
$S_{MNPQ}=\dfrac{S}{2}$.
Треугольники $ABC$ и $BMQ$ подобны с
коэффициентом $\dfrac{1}{2}$.
Следовательно,
$S_{BMQ}=\dfrac{1}{4}S_{BAC}$. Аналогично
$S_{DNP}=\dfrac{1}{4}S_{ACD}$.
Тогда
$S_{BMQ}+S_{DNP}=\dfrac{1}{4}(S_{ABC}+S_{ACD})=\dfrac{1}{4}S$.
Аналогично $S_{CNM}+S_{QAP}=\dfrac{1}{4}S$.
Тогда
$S_{MNPQ}=S-S_{BMQ}-S_{DNP}-S_{CNM}-S_{QAP}=S-\dfrac{1}{4}S-\dfrac{1}{4}S=\dfrac{1}{2}S$.
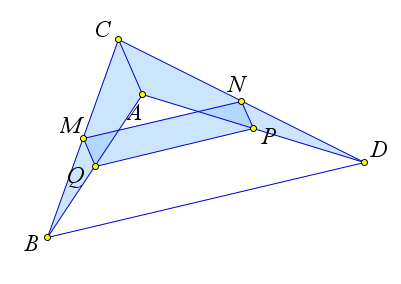
Второй случай
Рассмотрим случай, когда $ABCD$ – невыпуклый четырехугольник.
Аналогично первому
случаю $S_{BMQ}+S_{DNP}=\dfrac{1}{4}(S_{ABC}+S_{ACD})=\dfrac{1}{4}S$.
Обозначим $S_1=S_{BAD}$.
Тогда
$S_{CMN}=\frac{1}{4}S_{BCD}=\frac{1}{4}(S+S_1)$ и
$S_{QAP}=\frac{1}{4}S_1$.
Тогда $$S_{MNPQ}=S-S_{BMQ}-S_{NPD}-S_{CNM}+S_{AQP}=S-\dfrac{1}{4}S-\dfrac{1}{4}(S+S_1)+\dfrac{1}{4}S_1=\dfrac{1}{2}S.$$