Площади различных многоугольников

Площадь прямоугольника равна произведению его смежных сторон.

Рассмотрим прямоугольник $ABCD$ со сторонами $AB=a$ и $BC=b$.

Докажем, что его площадь $S=ab$.

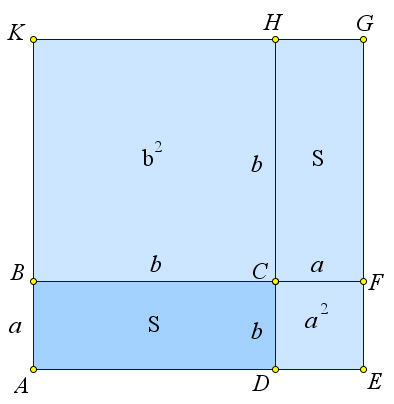
Достроим прямоугольник $ABCD$ до квадрата $AEGK$, продлив прямую $AD$ за точку $D$ на отрезок $DE=a$, и прямую $AB$ за точку $B$ на отрезок $BK=b$.

Тогда $BCHK$ и $CFED$ – это квадраты, и их площади равны соответственно $b^2$ и $a^2$.

Кроме того, $CFGH$ – это прямоугольник со сторонами $a$ и $b$, следовательно, его площадь равна площади $ABCD$.

Обозначим площадь $ABCD$ за $S$.

Тогда $S_{AEGK}=S_{BCHK}+S_{CFED}+2S=a^2+b^2+2S$.

С другой стороны $S_{AEGK}=(a+b)^2=a^2+b^2+2ab$.

Откуда получаем, что $2ab=2S$, то есть $S=ab$.

Площадь прямоугольного треугольника равна полупроизведению его катетов.

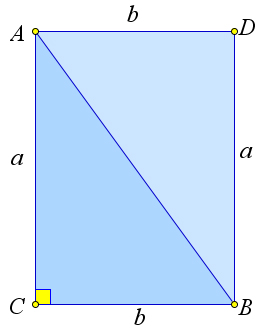
Рассмотрим прямоугольный треугольник $\triangle ABC$, в котором $BC=a, AC=b$ и $\a C=90^\circ$.

Докажем, что $S_{\triangle ABC}=\dfrac{ab}{2}$.

Достроим треугольник $\triangle ABC$ до прямоугольника $ADBC$.

Тогда $S_{ADBC}=ab=2S_{\triangle ABC}$.

Следовательно, $S_{\triangle ABC}=\dfrac{ab}{2}$.

Площадь треугольника равна половине произведения любой из его сторон и проведенной к ней высоты.

Рассмотрим треугольник $ABC$, в котором $BH$ – это высота.

Докажем, что $S_{ABC}=\dfrac{1}{2}\cdot BH\cdot AC.$

Возможны три случая:

1. точка $H$ совпадает с одним из концов отрезка $AC$, например с точкой $C$;
2. точка $H$ принадлежит отрезку $AC$ и не совпадает с его концами;
3. точка $H$ лежит за пределами отрезка $AH$.

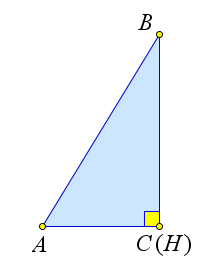
Пусть высота из точки $B$ падает в один из концов отрезка $AC$, например в вершину $C$.

Тогда $BC=BH$ и $\triangle ABC$ – прямоугольный, следовательно, по теореме получаем $S_{ABC}=\dfrac{1}{2}\cdot BH\cdot AC$.

Пусть высота $BH$ падает внутрь отрезка $AC$.

Тогда высота $BH$ разбивает треугольник $ABC$ на два прямоугольных треугольника $ABH$ и $BHC$, следовательно, $S_{ABC}=S_{ABH}+S_{BHC}=\dfrac{1}{2}\cdot BH\cdot AH+\dfrac{1}{2}\cdot BH\cdot HC=\dfrac{1}{2}\cdot BH\cdot (AH+HC)=\frac{1}{2}\cdot BH\cdot AC$.

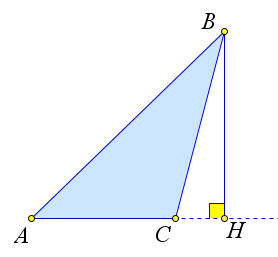
Пусть высота $BH$ падает вне отрезка $AC$, например за точку $C$.

Тогда

$S_{ABC}=S_{ABH}-S_{BCH}=\dfrac{1}{2}\cdot BH\cdot AH-\dfrac{1}{2}\cdot BH\cdot CH=\dfrac{1}{2}\cdot BH\cdot (AH-CH)=\dfrac{1}{2}\cdot BH\cdot AC$.

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

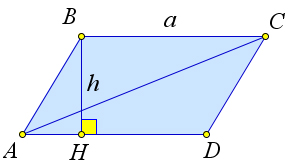
Рассмотрим параллелограмм $ABCD$, в котором сторона $AD=a$ и высота $BH=h$.

Докажем, что $S_{ABCD}=ah$.

Проведем диагональ $AC$.

По свойствам параллелограмма, диагональ делит его на два равных треугольника.

Следовательно, $S_{\triangle ABC}=S_{ADC}=\dfrac{1}{2}\cdot ah$.

Тогда $S_{ABCD}=2S_{ACD}=ah$.

Площадь трапеции равна произведению высоты на полусумму ее оснований.

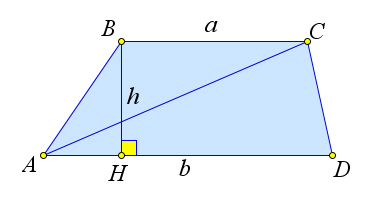
Рассмотрим трапецию $ABCD$, в которой $BH=h$ – высота, и основания $AD=a, BC=b$.

Докажем, что $S_{ABCD}=h\cdot\dfrac{a+b}{2}$.

Проведем диагональ $AC$.

Тогда $S_{\triangle ABD}=\dfrac{1}{2}\cdot ah$, $S_{\triangle BCD}=\dfrac{1}{2} ah$, поскольку высоты этих треугольников, проведенные к сторонам $AD$ и $BC$ соответственно, равны высоте трапеции.

Тогда $S_{ABCD}=S_{ABD}+S_{BCD}=\dfrac{1}{2}(ah+bh)=h\cdot\dfrac{a+b}{2}$.

Площадь ромба равна полупроизведению его диагоналей.

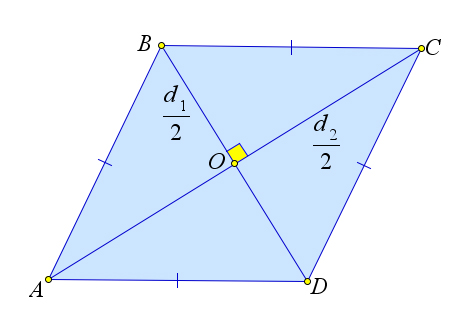
Рассмотрим ромб $ABCD$, в котором диагонали $AC=d_1$ и $BD=d_2$.

Докажем, что $S_{ABCD}=\dfrac{1}{2}\cdot d_1d_2$.

Пусть диагонали $AC$ и $BD$ пересекаются в точке $O$.

Диагонали разбивают ромб на четыре равных треугольника $\triangle ABO, \triangle BCO, \triangle CDO, \triangle DAO$.

Следовательно, $S_{ABCD}=4S_{ABO}=4\cdot\dfrac{1}{2}\dfrac{d_1}{2}\dfrac{d_2}{2}=\dfrac{1}{2}\cdot d_1d_2$.

Площадь выпуклого четырехугольника со взаимно перпендикулярными диагоналями равна полупроизведению его диагоналей.

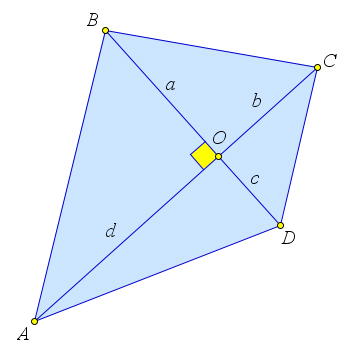
Рассмотрим четырехугольник $ABCD$ в котором $AC\perp BD$.

Пусть $AC$ пересекает $BD$ в точке $O$.

Обозначим $BO=a, CO=b, DO=c, AO=d$.

Тогда

$S_{ABCD}=S_{AOB}+S_{BOC}+S_{COD}+S_{AOD}=\dfrac{1}{2}ad+\dfrac{1}{2}ab+\dfrac{1}{2}bc+\dfrac{1}{2}cd=\dfrac{1}{2}(a(b+d)+c(b+d))=\dfrac{1}{2}(a+c)(b+d)=\dfrac{1}{2}AC\cdot BD$

Два треугольника, образованные боковыми сторонами трапеции и отрезками ее диагоналей, равны по площади.

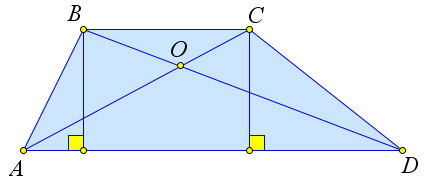
Рассмотрим трапецию $ABCD$, у которой диагонали $AC$ и $BD$ пересекаются в точке $O$.

Докажем, что $S_{\triangle AOB}=S_{\triangle COD}$.

Рассмотрим треугольники $\triangle ABD$ и $\triangle ACD$.

У этих треугольников общее основание $AD$, кроме того их высоты, проведенные к стороне $AD$ из точек $B$ и $C$ соответственно, тоже равны.

Следовательно, $S_{\triangle ABD}=S_{\triangle ACD}$.

Но тогда $S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle COD}$.