Многоугольной фигурой называется объединение конечного числа многоугольников.

Для многоугольных фигур площадью называется величина, обладающая свойствами:

1. Площадь неотрицательна.
2. Если фигура составлена из нескольких многоугольных фигур, то ее площадь равна сумме площадей этих фигур.
3. Равные фигуры имеют одну и ту же площадь.
4. Площадь единичного квадрата равна $1$.

Площадь квадрата со стороной $1$ называют квадратной единицей площади.

Площадь квадрата со стороной $a$ равна $a^2$.

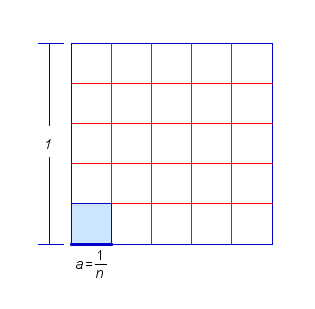
Начнем с того случая, когда $a=\dfrac{1}{n}$, где $n$ — целое число.

Возьмем квадрат со стороной 1 и разобьем его на $n^2$ равных квадратов, так как показано на рисунке.

Так как площадь большого квадрата равна $1$, то площадь каждого маленького квадрата равна $\dfrac{1}{n^2}$.

Сторона каждого маленького квадрата равна $\dfrac{1}{n}$, то есть $a$.

Итак, $S=\dfrac{1}{n^2}=\left(\dfrac{1}{n}\right)^2=a^2$.

Пусть теперь число $a$ представляет собой конечную десятичную дробь, содержащую $n$ знаков после запятой (в частности, число $a$ может быть целым, когда $n=0$).

Тогда число $m=a\cdot 10^n$ целое.

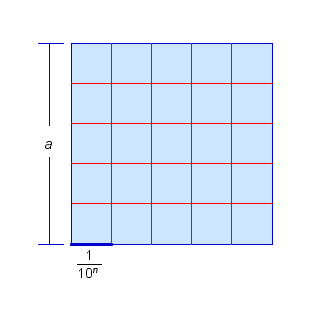
Разобьем данный квадрат со стороной $a$ на $m^2$ равных квадратов так, как показано на рисунке.

При этом каждая сторона данного квадрата разобьется на $m$ равных частей, и, значит, сторона любого маленького квадрата равна $\dfrac{a}{m}=\dfrac{a}{a\cdot 10^n}=\dfrac{1}{10^n}$.

По первому случаю площадь маленького квадрата равна $\left(\dfrac{1}{10^n}\right)^2$.

Следовательно, площадь $S$ данного квадрата равна $m^2\cdot \left(\dfrac{1}{10^n}\right)^2=\left(\dfrac{m}{10^n}\right)^2=\left(\dfrac{a\cdot 10^n}{10^n}\right)^2=a^2$.

Пусть число $a$ представляет собой бесконечную десятичную дробь.

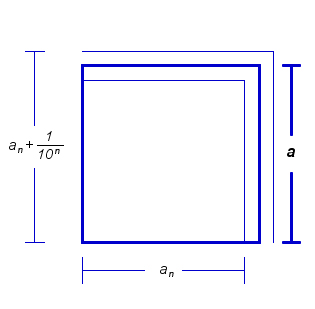
Рассмотрим число $a_n$, получаемое из $a$ отбрасыванием всех десятичных знаков после запятой, начиная с $(n+1)$-ого.

Так как число $a$ отличается от $a_n$ не более чем на $\dfrac{1}{10^n}$, то $a_n\leqslant a\leqslant a_n+\dfrac{1}{10^n}$.

Тогда $a_n^2\leqslant a^2\leqslant \left(a_n+\dfrac{1}{10^n}\right)^2\ \ (1)$.

Кроме того, ясно, что площадь $S$ данного квадрата заключена между площадью квадрата со стороной $a_n$ и площадью квадрата со стороной $a_n+\dfrac{1}{10^n}$, то есть между числами $a_n^2$ и $\left(a_n+\dfrac{1}{10^n}\right)^2$:

$a_n^2\leqslant S\leqslant \left(a_n+\dfrac{1}{10^n}\right)^2\ \ (2)$.

Будем неограниченно увеличивать число $n$.

Тогда число $\dfrac{1}{10^n}$ будет становиться сколь угодно малым, и, значит, число $\left(a_n+\dfrac{1}{10^n}\right)^2$ будет сколь угодно мало отличаться от числа $a_n^2$.

Поэтому из неравенств $(1)$ и $(2)$ следует, что число $S$ сколь угодно мало отличается от числа $a^2$.

Следовательно, эти числа равны $S=a^2$, что и требовалось доказать.