Правильные многоугольники

Многоугольник называется правильным, если все его стороны равны и все его углы равны.

В каждом правильном многоугольнике есть точка, равноудаленная от всех его сторон и от всех его вершин.

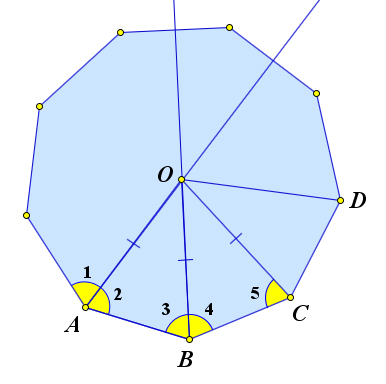
Рассмотрим правильный многоугольник.

Проведем в нём биссектрисы углов $A$ и $B$.

Пусть они пересекаются в точке $O$.

Докажем, что биссектрисы остальных углов данного многоугольника тоже проходят через точку $O$.

Так как $OA$ и $OB$ – это биссектрисы, а углы правильного многоугольника равны, то $\angle 1=\angle 2=\angle 3=\angle 4=\frac{1}{2}\angle A$.

Следовательно, треугольник $\triangle AOB$ равнобедренный, то есть $OA=OB$.

Кроме того $\triangle AOB=\triangle BOC$ по первому признаку равенства ($OA=OB, AB=BC, \angle 2=\angle 4$).

Следовательно, $OB=OC$ и $\angle 5=\angle 3=\frac{1}{2}\angle A$.

Таким образом $OC$ является биссектрисой угла $C$, а точка $O$ равноудалена от вершин $A, B$ и $C$.

Аналогичные рассуждение теперь можно провести для вершины $D$, и потом по очереди для всех других вершин многоугольника.

Таким образом точка $O$ равноудалена от всех вершин многоугольника, в силу равенства треугольников.

Кроме того точка $O$ равноудалена от всех сторон многоугольника, так как это точка пересечение биссектрис.

Для любого правильного многоугольника существует вписанная и описанная окружность, причём их центры совпадают. Вписанная и описанная окружность для правильного многоугольника единственны.

Существование и совпадение центров вписанной и описанной окружности непосредственно следуют из теоремы.

Докажем единственность.

Рассмотрим какие-нибудь три вершины многоугольника, например $A, B, C$.

Так как через эти точки проходит только одна окружность, то около многоугольника можно описать только одну окружность.

Теперь предположим, что в правильный многоугольник можно вписать окружность с центром $O$ и радиусом $OM$ и другую окружность с центром $O_1$ и радиусом $O_1M_1$.

Тогда центр $O_1$ равноудалён от всех сторон многоугольника, следовательно, точка $O_1$ лежит на каждой из биссектрис углов многоугольника и, следовательно, совпадает с точкой $O$ пересечения этих биссектрис.

Радиус окружности $O_1M_1$ равен расстоянию от точки $O$ до сторон многоугольника, то есть $OM$.

Таким образом вторая окружность совпадает с первой.

Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.

Утверждение следует из того, что радиус вписанной окружности является высотой равнобедренного треугольника $AOB$.

Пусть $\alpha$ – это угол правильного $n$-угольника, а $\beta$ – угол между радиусами описанной окружности, проведёнными к соседним вершинам. Тогда выполняются следующие соотношения

1. $\alpha=\frac{180^\circ(n-2)}{n},\ \beta=\frac{360^\circ}{n}$.
   
2. $a=2r\tg{\frac{\beta}{2}}=2r\ctg{\frac{\alpha}{2}}$.
   
3. $a=2R\sin{\frac{\beta}{2}}=2R\cos{\frac{\alpha}{2}}$.
   
4. $r=R\cos{\frac{\beta}{2}}=R\sin{\frac{\alpha}{2}}$.
   
5. $S=pr=\frac{1}{2}nR^2\sin{\beta}$.
   

По теореме сумма углов $n$-угольника равна $180^\circ(n-2)$, следовательно, каждый угол будет равен $\alpha=\dfrac{180^\circ(n-2)}{n}$.

Кроме того, полный угол $O$ разделён радиусами, проведёнными к вершинам многоугольника, на $n$ частей, следовательно, $\beta=\dfrac{360^\circ}{n}$.

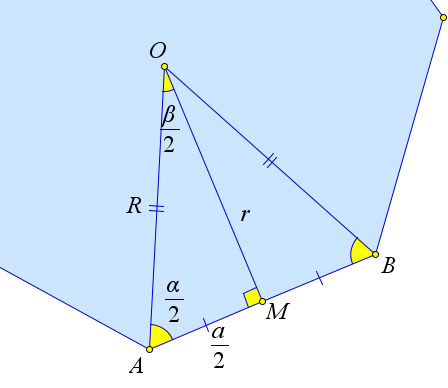
Проведем высоту $OM$ треугольника $AOB$.

Так как треугольник $AOB$ равнобедренный, то $\angle AOM=\dfrac{\beta}{2}$, $AM=\dfrac{a}{2}$.

Кроме того, $\angle OAM=\dfrac{\alpha}{2}$.

Из треугольника $AOM$ получаем $a=2r\tg{\dfrac{\beta}{2}}=2r\ctg{\dfrac{\alpha}{2}}$.

$\sin{\dfrac{\beta}{2}}=\cos{\dfrac{\alpha}{2}}=\dfrac{\frac{a}{2}}{R}$, следовательно, $a=2R\sin{\dfrac{\beta}{2}}=2R\cos{\dfrac{\alpha}{2}}$.

$\tg{\dfrac{\beta}{2}}=\ctg{\dfrac{\alpha}{2}}=\dfrac{\dfrac{a}{2}}{r}$, следовательно,

$\cos{\dfrac{\beta}{2}}=\sin{\dfrac{\alpha}{2}}=\dfrac{r}{R}$, следовательно, $r=R\cos{\dfrac{\beta}{2}}=R\sin{\dfrac{\alpha}{2}}$.

Известно, что $S=pr$ для любого описанного многоугольника, в том числе и для правильного. C другой стороны $S=n\cdot S_{AOB}=n\cdot\dfrac{1}{2}R^2\sin{\beta}$.

Периметры правильных $n$-угольников относятся как радиусы описанных около них окружностей.

Рассмотрим два правильных $n$-угольника со сторонами $a_n$ и $a'_n$ соответственно.

Используя формулы выпишем периметры $P_n$ и $P'_n$ данных многоугольников: $P_n=n\cdot a_n=n\cdot 2R\sin{\dfrac{180^\circ}{n}}, P'_n=n\cdot a'_n=n\cdot 2R'\sin{\dfrac{180^\circ}{n}}$.

Следовательно, $\dfrac{P_n}{P'_n}=\dfrac{2R}{2R'}=\dfrac{R}{R'}$.