Признаки равенства треугольников

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.

Треугольники называются равными, если их можно совместить наложением.

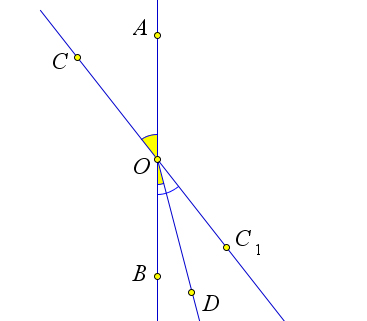
Пусть на прямой $AB$ точка $O$ лежит между точками $A$ и $B$. Если от лучей $OA$ и $OB$ в разные полуплоскости отложить лучи $OC$ и $OD$ соответственно так, чтобы $\angle COA=\angle DOB$, то точки $C, O$ и $D$ лежат на одной прямой.

Предположим противное.

Тогда продолжим луч $CO$ за точку $O$: получим луч $OC_1$

Тогда $\angle COA=\angle BOC_1$, как вертикальные, и от луча $OB$ отложены два равных угла $\angle DOB$ и $\angle COC_1$, что противоречит аксиоме.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

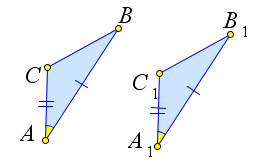
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $AB=A_1B_1, AC=A_1C_1, \angle A=\angle A_1$.

Докажем, что $\triangle ABC=\triangle A_1B_1C_1$.

Так как $\angle A=\angle A_1$, то согласно аксиоме треугольник $ABC$ можно наложить на треугольник $A_1B_1C_1$ так, что вершина $A$ совместиться с вершиной $A_1$, а стороны $AB$ и $AC$ наложатся соответственно на лучи $A_1B_1$ и $A_1C_1$.

В силу аксиомы, так как $AB=A_1B_1$ и $AC=A_1C_1$, то стороны $AB$ и $A_1B_1$, $AC$ и $A_1C_1$ совместиться.

В частности совместятся точки $B$ и $B_1$, $C$ и $C_1$.

Следовательно, по аксиоме совместятся и стороны $BC$ и $B_1C_1$.

Итак, треугольники $ABC$ и $A_1B_1C_1$ полностью совместились.

Следовательно, согласно определению, они равны.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

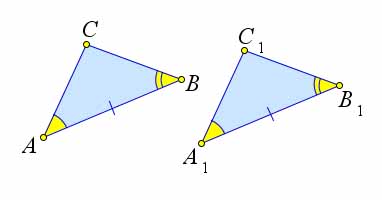
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $AB=A_1B_1, \angle A=\angle A_1, \angle B=\angle B_1$.

Докажем, что $\triangle ABC=\triangle A_1B_1C_1$.

Наложим треугольник $ABC$ на треугольник $A_1B_1C_1$ так, чтобы вершина $A$ совместилась с вершиной $A$, сторона $AB$ – с равной ей стороной $A_1B_1$, а вершины $C$ и $C_1$ оказались по одну сторону от прямой $A_1B_1$.

Так как $\angle A=\angle A_1$ и $\angle B=\angle B_1$, то по сторона $AC$ наложится на луч $A_1C_1$, а сторона $BC$ – на луч $B_1C_1$.

Поэтому вершина $C$ – общая точка сторон $AC$ и $BC$ – окажется как лежащей на луче $A_1C_1$, так и на луче $B_1C_1$ и, следовательно, совместиться с общей точкой этих лучей – вершиной $C_1$.

Значит, совместятся стороны $AC$ и $A_1C_1$, $BC$ и $B_1C_1$.

Итак треугольники $ABC$ и $A_1B_1C_1$ полностью совместятся.

Следовательно, они равны.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

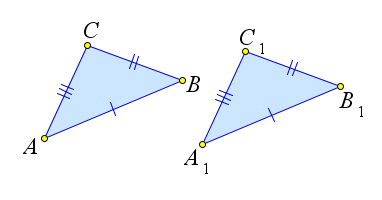
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $AB=A_1B_1, AC=A_1C_1, BC=B_1C_1$.

Докажем, что $\triangle ABC=\triangle A_1B_1C_1$.

Приложим треугольник $ABC$ к треугольнику $A_1B_1C_1$ так, чтобы вершина $A$ совместилась с вершиной $A_1$, вершина $B$ – C вершиной $B_1$, а вершины $C$ и $C_1$ оказались по разные стороны от прямой $A_1B_1$.

Возможны три случая:

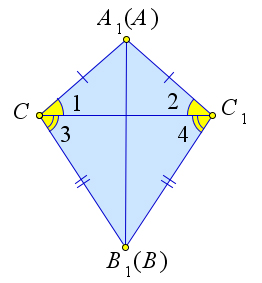
1. луч $C_1C$ проходит внутри угла $A_1C_1B_1$
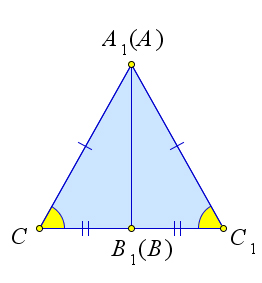
2. луч $C_1C$ совпадает с одной из сторон этого угла
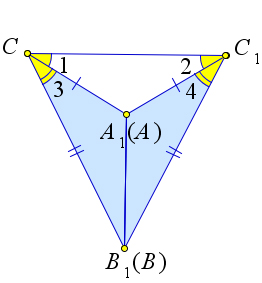
3. луч $C_1C$ проходит вне угла $A_1C_1B_1$.

По условию теоремы $AB=A_1B_1, AC=A_1C_1, BC=B_1C_1$, следовательно, треугольники $A_1C_1C$ и $B_1C_1C$ – равнобедренные.

По теореме $\angle 1=\angle 2, \angle 3=\angle 4$, поэтому $\angle A_1CB_1=\angle A_1C_1B_1$.

Итак, $AC=A_1C_1, BC=B_1C_1, \angle C=\angle C_1$.

Следовательно, треугольники $ABC$ и $A_1B_1C_1$ равны по первому признаку равенства треугольников.

Пусть луч $C_1C$ совпадает со стороной $C_1B$ угла $A_1C_1B_1$.

Тогда, так как $AC=A_1C_1$, то треугольник $СA_1C_1$ равнобедренный, и ,следовательно, $\angle C=\angle C_1$.

Тогда треугольники $A_1BC_1$ и $ABC$ равны по первому признаку равенства треугольников.

Третий случай доказывается аналогично первому.