Проекцией точки $M$ на прямую $a$ называется основание перпендикуляра, проведенного из точки $M$ к прямой $a$, если точка $M$ не лежит на прямой $a$, и сама точка $M$, если она лежит на прямой $a$.

Проекцией отрезка на прямую $a$ называется множество проекций всех точек этого отрезка на прямую $a$.

Проекцией отрезка, лежащего на одной из сторон острого угла на другую сторону является отрезок.

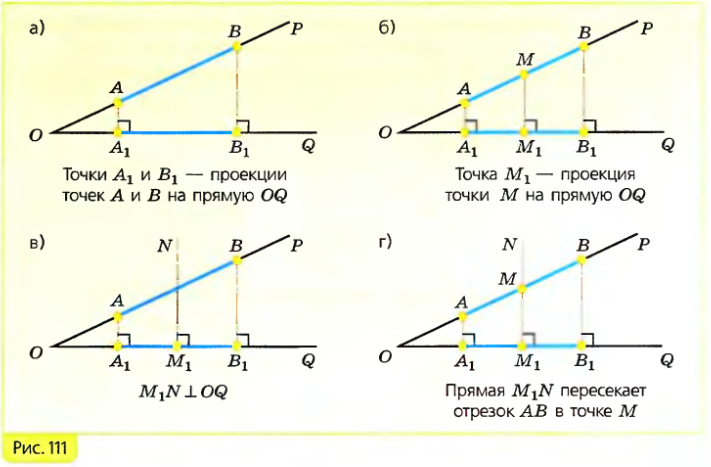
Рассмотрим острый угол $\angle POQ$ и отрезок $AB$, лежащий на стороне $OP$ этого угла (рис. 111, а). Пусть $A_1$ и $B_1$ – проекции точек $A$ и $B$ на прямую $OQ$.

Наглядно видно, что отрезок $A_1B_1$ является проекцией отрезка $AB$ на прямую $OQ$. Однако этот факт требует обоснования: нужно доказать, что проекция каждой точки отрезка $AB$ лежит на отрезке $A_1B_1$ и, обратно, каждая точка отрезка $A_1B_1$ является проекцией некоторой точки отрезка $AB$.

Начнем с доказательства первого утверждения.

Пусть $M_1$ – проекция точки $M$ отрезка $AB$ на прямую $OQ$ (рис. 111, б). Докажем, что точка $M_1$ лежит на отрезке $A_1B_1$. Так как прямые $AA_1$ и $MM_1$ перпендикулярны к прямой $OQ$, то они не пересекаются, поэтому точка $A_1$ лежит по ту же сторону от прямой $MM_1$, что и точка $A$. По аналогичной причине точка $B_1$ лежит по ту же сторону от прямой $MM_1$, поскольку эта прямая пересекает отрезок $AB$.

Следовательно, точки $A_1$ и $B_1$ также лежат по разные стороны от прямой $MM_1$, поэтому точка $M_1$ лежит между точками $A_1$ и $B_1$, т. е. лежит на отрезке $A_1B_1$. Первая часть утверждения доказана.

Пусть теперь $M_1$ – произвольная точка отрезка $A_1B_1$. Докажем, что она является проекцией некоторой точки отрезка $AB$. Проведем прямую $M_1N$, перпендикулярную прямой $OQ$ (рис. 111, в). Точки $A$ и $A_1$ лежат по одну сторону от этой прямой (поскольку прямые $AA_1$ и $M_1N$ не пересекаются), точки $B$ и $B_1$ также лежат по одну сторону от прямой $M_1N$, а точки $A_1$ и $B_1$ лежат по разные стороны от этой прямой. Следовательно, точка $A$ и $B$ также лежат по разные стороны от прямой $M_1N$, и поэтому прямая $M_1N$ пересекает отрезок $AB$ в некоторой точке $M$ (рис. 111, г). Проекцией этой точки на прямую $OQ$ и является точка $M_1$. Утверждение доказано.

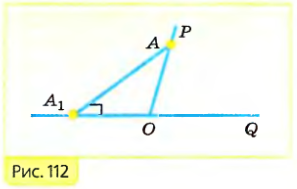
Отметим, что точка $A_1$ и $B_1$ лежат на стороне $OQ$ угла $POQ$, а не на ее продолжении. В самом деле, если предположить, что точка $A_1$ лежит на продолжении стороны $OQ$ (рис. 112), то получается треугольник $AA_1O$ с прямым углом $A_1$ и тупым углом $O$, чего не может быть.

Проекцией вектора $\overrightarrow{AB}$ на прямую $p$ называется вектор $\overrightarrow{A_1B_1}$, где $A_1$ и $B_1$ – это проекции точек $A$ и $B$ на прямую $p$. Проекцию вектора $\overrightarrow{AB}$ на прямую $p$ обозначают так: $\overrightarrow{A_1B_1}=pr_{p}{\overrightarrow{AB}}$ или так $\overrightarrow{A_1B_1}=\overrightarrow{pr_{p}{\overrightarrow{AB}}}$.

Углом между двумя ненулевыми векторами называется величина образуемого ими угла, когда они отложены от одной точки. Если векторы сонаправлены, то угол между ними считается равным $0^\circ$. Если векторы направлены противоположно, то угол между ними равен $180^\circ$.

Угол между векторами не зависит от выбора точки, от которой они откладываются.

Для коллинеарных векторов утверждение теоремы очевидно. Докажем теорему для неколлинеарных векторов.

Пусть $\vec{a}$ и $\vec{b}$ – два неколлинеарных вектора. Отложим их от точки $O$, тогда $\overrightarrow{OA}=\vec{a}, \overrightarrow{OB}=\vec{b}$, и от точки $O_1$, тогда $\overrightarrow{O_1A_1}=\vec{a}, \overrightarrow{O_1B_1}=\vec{b}$.

Пусть прямые $OA$ и $O_1B_1$ пересекаются в некоторой точке $O_2$. Обозначим буквой $\alpha$ тот угол с вершиной в точке $O_2$, который будет соответственным с углом $AOB$ (при параллельных $OB, O_2B_1$ и секущей $OO_2$).

По свойствам параллельных прямых $\alpha=\angle AOB$.

Но тот же угол $\alpha$ будет соответственным и для угла $A_1O_1B_1$ (при параллельных прямых $A_1O_1, AO_2$ и секущей $O_1O_2$). Поэтому (по тому же свойству) $\alpha=\angle A_1O_1B_1$.

Следовательно, $\angle A_1O_1B_1=\angle AOB$.

Координатная ось – это прямая (обозначим её $x$), на которой выбраны точка $O$ – начало координат, и точка $E$, такая что $|OE|=1$. Вектор $\overrightarrow{OE}=\vec{e}$ – называют единичным вектором оси $x$; направление оси $x$ задаётся её единичным вектором.

Координатой точки $M$, лежащей на оси $x$, называется такое число $x_M$, что $\overrightarrow{OM}=x_M\cdot \vec{e}$, где $\vec{e}$ – единичный вектор оси $x$.

Проекцией $v_x$ вектора $\vec{v}=\overrightarrow{AB}$ на ось $x$ называется длина отрезка $A_1B_1$ взятая со знаком «плюс» или «минус». Точки $A_1$ и $B_1$ – проекции точек $A$ и $B$ на ось $x$. При этом знак «плюс» берётся, если направление вектора $\overrightarrow{A_1B_1}$ совпадает с направлением оси $x$, и знак «минус», если эти направления противоположны. Если $\overrightarrow{A_1B_1}=\vec{0}$, то есть $A_1=B_1$, то $v_x=0$.

Векторная и числовая проекции вектора $\vec{v}$ на ось $x$ с единичным вектором $\vec{e}$ связаны соотношением $\overrightarrow{pr_{x}\vec{v}}=v_x\cdot\vec{e}$.

…

Если точки $A$ и $B$ лежат на оси $x$ и имеют координаты $x_A$ и $x_B$ соответственно, то $|AB|=|x_B-x_A|$ вне зависимости от расположения точек $A$ и $B$ на оси.

…

Проекция вектора $\vec{v}=\overrightarrow{AB}$ на ось $x$ равна $v_x=x_B-x_A$, где $x_A$ и $x_B$ – координаты проекций точек $A$ и $B$ на ось $x$.

Пусть проекциями точек $A$ и $B$ на ось $x$ являются точки $A_1$ и $B_1$ соответственно. ОбозначимИзвестно, что $|A_1B_1|=x_B-x_A$.

Если $\overrightarrow{A_1B_1}\neq\vec{0}$ и $\overrightarrow{A_1B_1}\upuparrows \vec{e}$, то $x_B>X_A$ и $x_B-x_A>0$. В этом случае $|x_B-x_A|=x_B-x_A$ и $v_x=|\overrightarrow{A_1B_1}|=x_B-x_A$.

Если $\overrightarrow{A_1B_1}\updownarrows \vec{e}$, то $x_B<x_A$ и $x_B-x_A<0$. В этом случае $|x_B-x_A|=-(x_B-x_A)$ и $v_x=-|\overrightarrow{A_1B_1}|=x_B-x_A$.

Если $\overrightarrow{A_1B_1}=\vec{0}$, то $v_x=0, A_1=B_1, x_B=x_A$ и снова $v_x=x_B-x_A$.

Итак, во всех случаях $v_x=x_B-x_A$.

Углом между вектором и координатной осью называется угол между вектором и единичным вектором этой оси.

Проекция ненулевого вектора на ось равна длине этого вектора, умноженной на косинус угла между этим вектором и осью.

Пусть дан вектор $\vec{v}=\overrightarrow{AB}\neq\vec{0}$, $\vec{e}$ – единичный вектор координатной оси $x$, и $\varphi=\angle(\vec{v}, \vec{e})$.

Докажем, что проекция $v_x$ вектора $\vec{v}$ на ось $x$ вычисляется по формуле $v_x=|\vec{v}|\cos{\varphi}$ $(1)$.

Возможны следующие случаи:

1) Угол $\varphi = 0^\circ$. Тогда $\overrightarrow{AB}=\vec{e}$, $\overrightarrow{A_1B_1}=\overrightarrow{AB}=\vec{v}$ и $v_x=|\vec{v}|$. Так как $\cos{0^\circ}$=1, то $v_x=|\vec{v}|\cos{\varphi}$.

2) Угол $\varphi$ острый. Пусть точка $A$ не лежит на оси $x$. Через точку $A$ проведем прямую $p$, параллельную оси $x$. Пусть точка $C$ – проекция точки $B$ на прямую $p$. Получим прямоугольный треугольник $ABC$ с углом $\varphi$ при вершине $A$ и прямоугольник $AA_1B_1C$. Тогда $v_x=|\overrightarrow{A_1B_1}|=AC=AB\cos{\varphi}=|\vec{v}|\cos{\varphi}$, то есть $v_x=|\vec{v}|\cos{\varphi}$.

Если точка $A$ лежит на оси $x$? то равенство $(1)$ вытекает из прямоугольного треугольника $ABB_1$.

3) Угол $\varphi=90^\circ$. В этом случае $\overrightarrow{AB}=\vec{e}$, $A_1=B_1$ и $v_x=0$. И так как $\cos{90^\circ}=0$, то равенство $(1)$ выполняется.

4) Угол $\varphi$ тупой. Сначала через точку $A$ проводим прямую $p$, параллельную оси $x$, и проецируем на нее точку $B$ в точку $C$юСнова получим прямоугольный треугольник $ABC$. Его угол при вершине $A$ равен $180^\circ-\varphi$. Поэтому $AC=AB\cos{(180^\circ-\varphi)}=-AB\cos{\varphi}$. В рассматриваемом случае $\overrightarrow{A_1B_1}\updownarrows\vec{e}$, и поэтому $v_x=-|\overrightarrow{A_1B_1}|=-AC=AB\cos{\varphi}=|\vec{v}\cos{\varphi}|$, то есть снова выполняется равенство $(1)$.

Если же точка $A$ лежит на прямой $x$ то доказательство только упрощается соответственным образом.

5) Угол $\varphi=180^\circ$. Тогда $\overrightarrow{AB}\updownarrows\vec{e}$, $\overrightarrow{A_1B_1}=\overrightarrow{AB}=\vec{v}$ и $v_x=-|\vec{v}|$. Так как $\cos{180^\circ}=-1$, то равенство $(1)$ снова имеет место.

Равные векторы имеют равные проекции на заданную ось.

Проекция вектора $\vec{v}$ зависит лишь от длины этого вектора и угла $\varphi$, который он образует с данной осью, так как $v_x=|\vec{v}|\cos{\varphi}$. Равные же векторы имеют, во-первых, равные длины и, во-вторых, образуют с осью один и тот же угол (в силу параллельности прямых). Следовательно, их проекции равны.

При сложении векторов их проекции на ось складываются.

Сложим любые два вектора $\vec{a}=\overrightarrow{AB}$ и $\vec{b}=\overrightarrow{BC}$. Получим вектор $\vec{c}=\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$. Пусть точки $A_1, B_1, C_1$ – проекции точек $A, B, C$ на ось $x$, а $x_A, x_B, x_C$ – их координатыб и $a_x, b_x, c_x$ – проекции векторов $\vec{a}, \vec{b}, \vec{c}$ на ось $x$.

Так как $a_x=x_B-x_A, b_x=x_C-x_B$, то $a_x+b_x=x_B-x_A+x_C-x_B=x_C-x_A$.

C другой стороны $c_x=x_C-x_A$.

Поэтому $c_x=a_x+b_x$.

При умножении вектора на число его проекция умножается на это число.

Пусть $x$ – ось с начальной точкой $O$ и единичным вектором $\vec{e}$. Возьмем любой вектор $\vec{a}$ и отложим его от точки $O$: $\overrightarrow{OA}=\vec{a}$. Пусть $\varphi$ – угол между векторами $\vec{a}$ и $\vec{e}$. Умножим вектор $\vec{a}$ на число $\alpha$. Получим вектор $\vec{b}=\overrightarrow{OB}=\alpha\vec{a}$. Необходимо доказать, что $b_x=\alpha a_x$.

Возможны следующие случаи:

1) $\alpha>0$. Тогда $\angle(\vec{b},\vec{e})=\varphi$. Кроме того, $|\vec{b}|=|\alpha||\vec{a}|$, то есть $OB=\alpha OA$. Поэтому $b_x=|\vec{b}|\cos{\varphi}=OB\cos{\varphi}=\alpha OA\cos{\varphi}=\alpha a_x$.

2) $\alpha<0$. Тогда $\angle(\vec{b},\vec{e})=180^\circ-\varphi$. Кроме того, $|\vec{b}|=|\alpha||\vec{a}|$, то есть $OB=|\alpha| OA$. А так как $\alpha<0$, то $|\alpha|=-\alpha$ и поэтому $OB=-\alpha OA$. Следовательно, $b_x=|\vec{b}|\cos{(180^\circ-\varphi)}=-OB\cos{\varphi}=\alpha OA\cos{\varphi}=\alpha a_x$.

3) $\alpha=0$. Тогда $\vec{b}=\alpha \vec{a}=\vec{0}$, и поэтому $b_x=0$ и $b_x=\alpha a_x$.

Проекция линейной комбинации векторов, равна соответствующей линейной комбинации проекций этих векторов.