Пропорциональные отрезки в круге

Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.

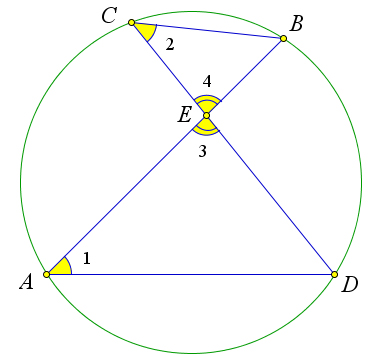
Пусть в окружности хорды $AB$ и $CD$ пересекаются в точке $E$.

Докажем, что $AE\cdot EB=CE\cdot ED$.

Рассмотрим треугольники $ADE$ и $CBE$.

В этих треугольниках $\angle 1=\angle 2=\frac{1}{2}\buildrel\,\,\frown\over{BD}$, так как они вписанные.

Кроме того $\angle 3=\angle 4$, как вертикальные.

Следовательно, $\triangle ADE\sim\triangle CBE$ по первому признаку подобия.

Отсюда $\dfrac{AE}{CE}=\dfrac{DE}{BE}$, или $AE\cdot EB=CE\cdot ED$.

Если через точку $M$ проведена касательная $MK$ ($K$ – точка касания) и секущая, пересекающая окружность в точках $A$ и $B$, то $MK^2=MA\cdot MB$.

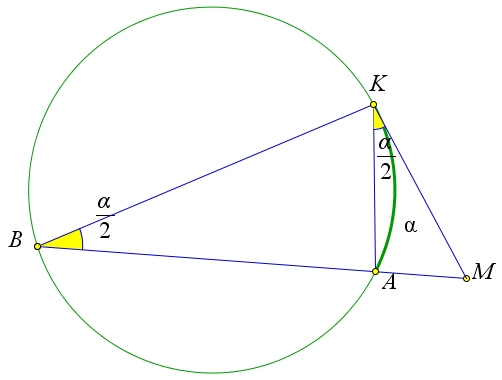
Пусть из точки $M$ к окружности проведены касательная $MK$ и секущая $MB$, пересекающая окружность в точке $A$.

Докажем, что $MK^2=MA\cdot MB$.

Обозначим $\alpha=\arc{AK}$.

Тогда $\angle B=\dfrac{\alpha}{2}$.

Кроме того $\angle MKA=\dfrac{\alpha}{2}$, как угол между касательной и хордой.

Тогда $\triangle MKA\sim\triangle MKB$ по первому признаку подобия ($\angle B=\angle MKA$, $\angle M$ – общий).

Тогда $\dfrac{KM}{AM}=\dfrac{BM}{KM}$, или $KM^2=AM\cdot BM$.

Если через точку $M$ проведены две секущие, одна из которых пересекает окружность в точках $A$ и $B$, а другая – в точках $C$ и $D$, то $MA\cdot MB=MC\cdot MD$.

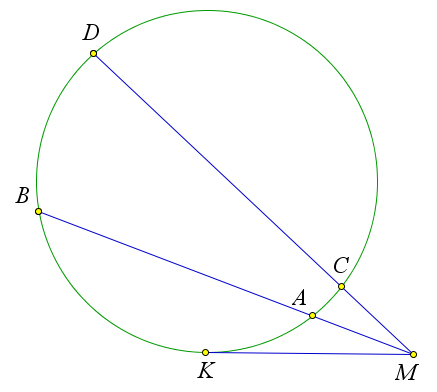
Пусть через точку $M$ проведены две секущие, одна из которых пересекает окружность в точках $A$ и $B$, а другая – в точках $C$ и $D$.

Докажем что $MA\cdot MB=MC\cdot MD$.

Проведем из точки $M$ к данной окружности касательную $MK$.

По теореме $MK^2=MA\cdot MB$ и $MK^2=MC\cdot MD$, откуда $MA\cdot MB=MC\cdot MD$.

Пусть через точку $M$ проведена прямая, пересекающая данную окружность в точках $A$ и $B$. Степенью точки $M$ относительно данной окружности называется произведение $MA\cdot MB$.

Степень точки относительно данной окружность не зависит от выбора прямой.

Эта теорема является прямым следствием предыдущих трёх теорем.