1. По двум катетам.
2. По гипотенузе и острому углу.
3. По катету и прилежащему острому углу.
4. По катету и гипотенузе.

Первый пункт теоремы верен, так как между катетами таких треугольников будут заключены равные между собой прямые углы, и треугольники будут равны по первому признаку равенства.

Второй и третий пункты теоремы верны, так как если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то их вторые острые углы тоже будут равны.

Тогда треугольники будут равны по второму признаку равенства.

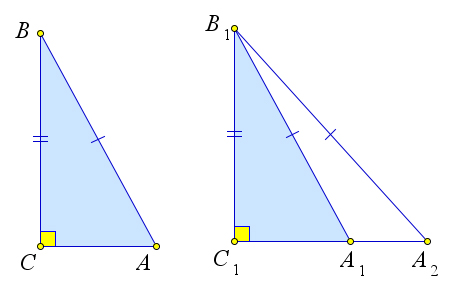
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $\angle C=\angle C_1=90^\circ, AB=A_1B_1, BC=B_1C_1$.

Докажем, что $\triangle ABC=\triangle A_1B_1C_1$.

Так как $\angle C=\angle C_1$, то треугольник $ABC$ можно наложить на треугольник $A_1B_1C_1$ так, что вершина $C$ совместиться с вершиной $C_1$, а стороны $CA$ и $CB$ наложатся на лучи $C_1A$ и $C_1B$.

Поскольку $CB=C_1B_1$, то вершина $B$ наложится на вершину $B_1$.

Докажем, что вершина $A$ наложится на вершину $A_1$.

Действительно, если предположить, что точка $A$ совместиться с некоторой точкой $A_2$ луча $C_1A_1$, то получится, что треугольник $A_1B_1A_2$ – равнобедренный, и, следовательно, $\angle A_1=\angle A_2$.

Но это невозможно, так как $\angle A_2$ – острый (как угол прямоугольного треугольника $B_1C_1A_2$), а $\angle A_1$ – тупой ( как смежный с острым углом $\angle C_1A_1B_1$).

Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $\angle C=\angle C_1=90^\circ, AB=A_1B_1, BC=B_1C_1$.

Докажем, что $\triangle ABC=\triangle A_1B_1C_1$.

Действительно по теореме Пифагора $AC=\sqrt{AB^2-BC^2}=\sqrt{A_1B_1^2-B_1C_1^2}=A_1C_1$.

Тогда треугольники $ABC$ и $A_1B_1C_1$ равны по третьему признаку равенства.