Если $O$ - центр описанной окружности $\triangle ABC$, то $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$.

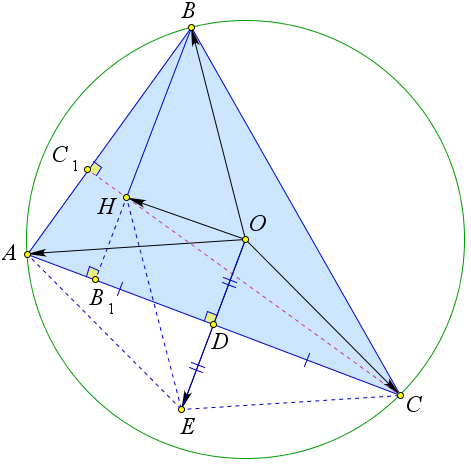
Рассмотрим треугольник $ABC$, в котором точка $O$ – центр описанной окружности, точка $H$ – ортоцентр, $D$ – середина стороны $AC$, $BB_1$ – высота.

Отложим на серединном перпендикуляре $OD$ точку $E$ так, чтобы $DE=OD$.

Тогда $AOCE$ – параллелограмм (так как диагонали точкой пересечения делятся пополам), а, следовательно, $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OE}$.

Кроме того прямые $BH$ и $OE$ перпендикулярны стороне $BC$, следовательно $BH\parallel OE$.

Кроме того по теореме \ref{117} $BH=2OD=OE$.

Следовательно, $BOEH$ – параллелограмм, а значит $\overrightarrow{OB}+\overrightarrow{OE}=\overrightarrow{OH}$.

Таким образом $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}$.

$OH=\sqrt{9R^2-(a^2+b^2+c^2)}$ , где $R$ – радиус описанной окружности; $a,b,c$ – длины сторон треугольника.

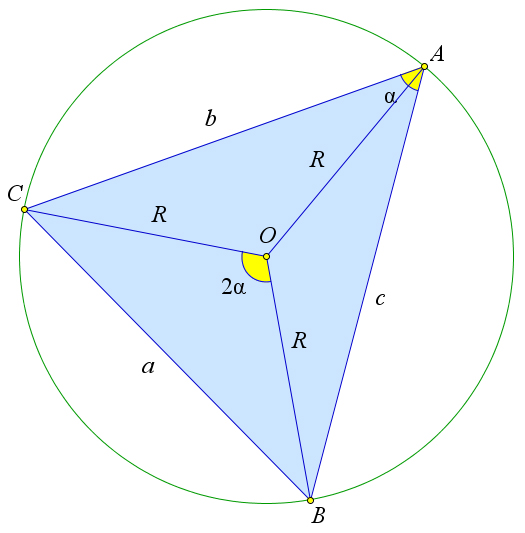
Рассмотрим остроугольный треугольник $ABC$, около которого описана окружность с центром $O$. Центральный угол $BOC$ и вписанный угол $BAC$ опираются на дугу $BC$, поэтому $\angle BAC=2\cdot\angle BOC$. Кроме того по обобщённой теореме синусов верны соотношения $a=2R\sin{A}, b=2R\sin{B}, c=2R\sin{\gamma}$. Учитывая эти соотношения, а так же теорему \ref{119}, получаем

$OH^2=\overrightarrow{OH}^2=(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})^2=$

$=OA^2+OB^2+OC^2+2\overrightarrow{OA}\cdot\overrightarrow{OB}+2\overrightarrow{OA}\cdot \overrightarrow{OC}+2\overrightarrow{OB}\cdot \overrightarrow{OC}=$

$=3R^2+2R^2\cos{2A}+2R^2\cos{2B}+2R^2\cos{2C}=$

$=3R^2+2R^2(1-2\sin^2{A})+2R^2(1-2\sin^2{B})+2R^2(1-2\sin^2{C})=$

$=9R^2-(4R^2\sin^2{A}+4R^2\sin^2{B}+4R^2\sin^2{C})=9R^2-(a^2+b^2+c^2).$

Если треугольник тупоугольный с тупым углом $\angle A$, то $\angle BAC=360^\circ-2\cdot\angle BOC$, но доказательства это не меняет, так как $ \cos{(360^\circ-2x)} = \cos{2x}$.

Если треугольник прямоугольный с прямым углом $\angle A$, то $\angle BOC = 180^\circ = 2\cdot \angle A$, и доказательство не меняется.

С учетом теоремы о прямой Эйлера, получаем:

$OZ = \dfrac{1}{3}\sqrt{9R^2-(a^2+b^2+c^2)}$
$ZH = \dfrac{2}{3}\sqrt{9R^2-(a^2+b^2+c^2)}$