Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

Средняя линия треугольника параллельна стороне треугольника и равна ее половине.

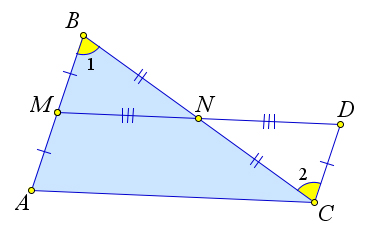
Рассмотрим $\triangle ABC$, с основанием $AC$ и средней линией $MN$.

Докажем, что $MN\parallel AC$ и $MN=\dfrac{1}{2}\cdot AC$.

На прямой $MN$ за точкой $N$ выберем точку $D$ так, чтобы выполнялось $MN=ND$.

Тогда $\triangle BMN=\triangle NDC$ по первому признаку равенства ($BN=NC, MN=ND$, $\angle BNM=\angle DNC$).

Тогда $\angle 1=\angle 2$, следовательно, $AB\parallel DC$.

Кроме того, из равенства треугольников следует, что $MB=DC$.

Но $MB=MA$, следовательно $MA=DC$.

Тогда $AMDC$ – параллелограмм ($DC=MA$, $MA\parallel DC$).

Следовательно, $MD\parallel AC$ и $AC=MD=2\cdot MN$.

1. Если в треугольнике $ABC$ точка $M$ – середина стороны $AB$, а точка $N$ принадлежит стороне $BC$, и при этом $MN\parallel AC$, то $MN$ – средняя линия.
2. Если в треугольнике $ABC$ точки $M$ и $N$ принадлежат сторонам $AB$ и $BC$ соответственно, при этом $MN\parallel AC$ и $2|MN|=|AC|$, то $MN$ – средняя линия.

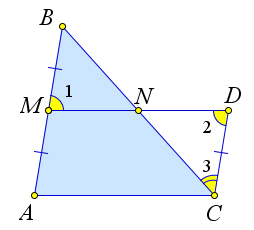
Рассмотрим $\triangle ABC$, в котором $M$ – середина $AB$, $N$ лежит на стороне $BC$, $MN\parallel AC$.

Докажем, что $MN$ – средняя линия.

Выберем на прямой $MN$ за точкой $N$ такую точку $D$, что $MD=AC$.

Тогда $AMDC$ – параллелограмм ($AC=MD$, $AC\parallel MD$).

Следовательно, $\angle B=\angle 3, \angle 1=\angle 2$, так как $AM\parallel CD$.

Кроме того $AM=DC$, как противоположные стороны параллелограмма.

Следовательно, $BM=MA=DC$.

Тогда $\triangle BMN=\triangle NDC$ по второму признаку равенства.

Следовательно, $BN=NC$, то есть $MN$ – средняя линия.

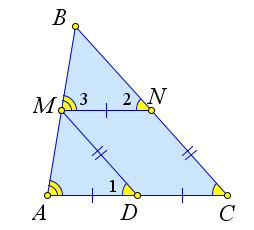
Рассмотрим треугольник $ABC$, в котором на сторонах $AB$ и $BC$ взяты точки $M$ и $N$ соответственно так, что $MN\parallel AC$ и $2\cdot MN=AC$.

Докажем, что тогда $MN$ – средняя линия треугольника $ABC$.

Пусть $D$ – это середина $AC$. Тогда $MNCD$ – параллелограмм ($MN=DC$, $MN\parallel DC$).

Следовательно, $MD\parallel NC$.

Тогда $\angle 1=\angle C=\angle 2$, как соответственные при параллельных прямых.

Кроме того $\angle A=\angle 3$.

Следовательно, $\triangle BMN=\triangle AMD$ по второму признаку равенства.

Тогда $BM=MA$ и $BN=MD=NC$, то есть $MN$ – средняя линия $\triangle ABC$.

Третий признак средней линии неверен.