1. Синус каждого угла не больше единицы.
2. При возрастании угла от $0^\circ$ до $90^\circ$ его синус возрастает от 0 до 1.
3. При возрастании угла от $90^\circ$ до $180^\circ$ его синус убывает от 1 до 0.
4. $\sin{(180^\circ-\alpha)}=\sin{\alpha}$.
5. Величина острого угла определяется его синусом.

Первый пункт следует из того, что перпендикуляр короче наклонной.

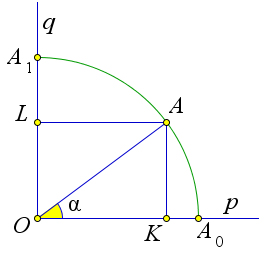
Возьмем прямой угол $O$ со сторонами $p$ и $q$.

Из вершины $O$ внутрь этого угла проведем единичный отрезок $OA$, образующий с лучом $p$ острый угол $\alpha$.

Из точки $A$ опустим перпендикуляры $AK$ и $AL$ на лучи $p$ и $q$.

Получим прямоугольник $OKAL$.

Так как $OA=1$, то $AK=\sin{\alpha}$.

А поскольку $OL=AK$, то $OL=\sin{\alpha}$.

Итак $\sin{\alpha}$ равен длине проекции $OL$ единичного отрезка $OA$ на луч $q$.

Когда угол $\alpha$ возрастает от $0^\circ$ до $90^\circ$, отрезок $OA$ поворачивается вокруг точки $O$ от положения $OA_0$ на луче $p$ до положения $OA_1$ на луче $q$.

Точка $A$ пробегает четверть окружности.

При этом точка $L$ движется от точки $O$ до точки $A_1$.

Длина отрезка $OL$, то есть $\sin{\alpha}$ возрастает от $0$ до $1$.

Когда тупой угол возрастает от $90^\circ$ до $180^\circ$, смежный ему острый угол убывает от $90^\circ$ до $0^\circ$.

В этом случае по пункту 2 синус такого угла убывает от $1$ до $0$.

Пусть $\sin{\alpha}=\sin{\beta}$.

Докажем, что тогда $\alpha=\beta$.

Действительно, возможно три случая:

1. $\alpha>\beta$. Тогда по пункту 2 $\sin{\alpha}>\sin{\beta}$. Значит, этот случай не имеет места.
2. $\alpha<\beta$. Тогда по пункту 2 $\sin{\alpha}<\sin{\beta}$. Значит, этот случай не имеет места.
3. Следовательно, остаётся только третья возможность: $\alpha=\beta$.