Содержание
Теорема о сумме углов треугольника и следствия из нее
Теорема
Доказательство
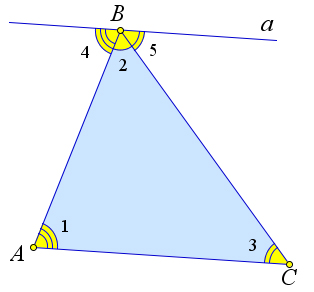
Рассмотрим произвольный треугольник $ABC$.
Докажем, что $\angle A+\angle B+\angle C=180^\circ$.
Проведем через вершину $B$ прямую $a$, параллельную стороне $AC$.
Тогда $\angle 1=\angle 4, \angle 3=\angle 5$, как накрест лежащие.
Тогда $\angle1 + \angle 2+\angle 3=\angle 4+\angle 2+\angle 5=180^\circ$.
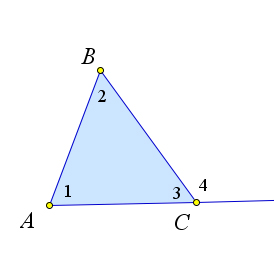
Следствие
Доказательство
Углы $\angle 3$ и $\angle 4$ смежные, поэтому $\angle 4=180^\circ-\angle 3=180^\circ-(180^\circ-\angle1-\angle 2)=\angle 1+\angle2$.
Теорема
Если биссектрисы углов $B$ и $C$ треугольника $ABC$ пересекаются в точке $M$, то $\angle BMC=90^\circ+\frac{1}{2}\angle A$.
Теорема
Биссектрисы смежных углов взаимно перпендикулярны.
Следствие
Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.