От любой точки $M$ можно отложить вектор, равный данному вектору $\vec{a}$, и при том только один.

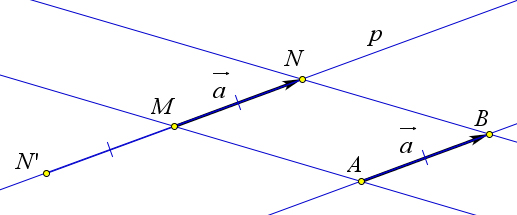
Рассмотрим вектор $\overrightarrow{AB}=\vec{a}$.

Проведем через точку $M$ прямую $p$, параллельную $AB$ (если $M$ – точка прямой $AB$, то в качестве прямой $p$ возьмём саму прямую $AB$).

На прямой $p$ отложим отрезки $MN$ и $MN'$, равные отрезку $AB$, и выберем из векторов $MN$ и $MN'$ тот, который сонаправлен с вектором $a$.

Этот вектор и является искомым вектором, равным вектору $a$.

Единственность следует из аксиомы об откладывании отрезка и аксиомы о параллельных прямых.