Содержание
Теорема Чевы
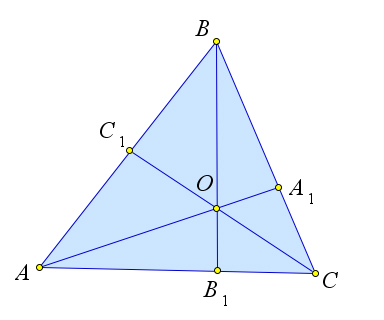
Чевианы $AA_1, BB_1$ и $CC_1$ треугольника $ABC$ пересекаются в одной точке тогда и только тогда, когда $\dfrac{AC_1}{C_1B}\cdot\dfrac{BA_1}{A_1C}\cdot\dfrac{CB_1}{B_1A}=1$.
Доказательство.
Докажем прямую теорему.
Рассмотрим треугольник $ABC$, в котором чевианы $AA_1, BB_1$ и
$CC_1$ пересекаются в точке $O$.
Докажем, что тогда
$\dfrac{AC_1}{C_1B}\cdot\dfrac{BA_1}{A_1C}\cdot\dfrac{CB_1}{B_1A}=1$.
Треугольники $AOB$ и $BOC$ имеют общее основание $BO$,
следовательно, их площади относятся, как высоты проведенные из
вершин $A$ и $C$ соответственно.
Треугольники $AOB_1$ и $B_1OC$ имеют общее основание $B_1O$, следовательно, их площади относятся,
как высоты проведенные из вершин $A$ и $C$ соответственно.
Следовательно $\dfrac{S_{AOB}}{S_{BOC}}=\dfrac{S_{AOB_1}}{S_{B_1OC}}$.
Кроме того, треугольники $AOB_1$ и $COB_1$ имеют общую высоту,
проведенную из вершины $O$, следовательно,
$\dfrac{S_{AOB_1}}{S_{B_1OC}}=\dfrac{AB_1}{B_1C}$.
Тогда $\dfrac{S_{AOB}}{S_{BOC}}=\dfrac{AB_1}{B_1C}$.
Аналогично $\dfrac{S_{AOC}}{S_{AOB}}=\dfrac{CA_1}{A_1B}$ и
$\dfrac{S_{BOC}}{S_{AOC}}=\dfrac{BC_1}{C_1A}$.
Перемножая эти
равенства, получим:
$\dfrac{AB_1}{B_1C}\cdot\dfrac{CA_1}{A_1B}\cdot\dfrac{BC_1}{C_1A}=\dfrac{S_{AOB}}{S_{BOC}}\cdot\dfrac{S_{AOC}}{S_{AOB}}\cdot\dfrac{S_{BOC}}{S_{AOC}}=1$.
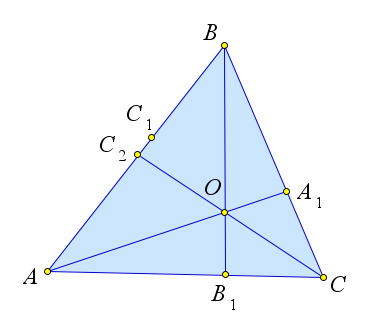
Докажем обратную теорему.
Пусть $O$ – точка пересечения чевиан
$AA_1$ и $BB_1$ в треугольнике $ABC$.
Пусть прямая $CO$ пересекает
сторону $AB$ в точке $C_2$.
Докажем, что если
$\dfrac{AC_1}{C_1B}\cdot\dfrac{BA_1}{A_1C}\cdot\dfrac{CB_1}{B_1A}=1$,
то $C_2=C_1$.
Так как чевианы $AA_1, BB_1$ и $CC_2$ пересекаются
в одной точке, то по первой части доказательства
$\dfrac{AC_2}{C_2B}\cdot\dfrac{BA_1}{A_1C}\cdot\dfrac{CB_1}{B_1A}=1$.
Но тогда $\dfrac{AC_2}{C_2B}=\dfrac{A_1C}{BA_1}\cdot\dfrac{B_1A}{CB_1}=\dfrac{AC_1}{C_1B}{}$, что и означает, что $C_1=C_2$.
Замечание
Можно доказать через теорему Менелая или через подобие.