Теорема косинусов
В каждом треугольнике квадрат любой его стороны равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Доказательство
Первый способ.
Рассмотрим треугольник $ABC$ со сторонами $a,b$ и $c$.
Докажем, что $c^2=a^2+b^2-2ab\cos{C}$.
Возможны три случая:
- $\angle C=90^\circ$
- $\angle C<90^\circ$
- $\angle C>90^\circ$.
Первый случай.
Пусть $\angle C=90^\circ$.
Тогда $\cos C=0$ и требуемое равенство обращается в теорему Пифагора для прямоугольного треугольника $ABC$.
Второй случай.
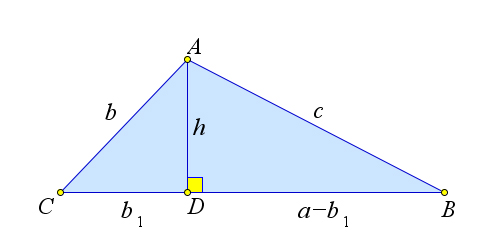
Пусть $\angle C<90^\circ$.
В треугольнике $ABC$ есть ещё хотя бы один острый угол.
Пусть это будет угол $B$.
Из вершины $A$ проведем высоту $AD$.
Так как углы $B$ и $C$ острые, точка $D$ лежит на стороне $BC$.
Отрезок $CD=b_1$ будет катетом в прямоугольном треугольнике $ACD$ с гипотенузой $AC=b$ и прилежащим острым углом $C$.
Поэтому $b_1=b\cos{C}.$
По теореме Пифагора находим $c^2$ из другого прямоугольного треугольника $ABD$ с катетами $AD=h$ и $BD=a-b_1$.
Получаем $c^2=(a-b_1)^2+h^2$.
Но $h^2=b^2-b_1^2$ из треугольника $ACD$.
Подставив это выражение для $h^2$ в предыдущее равенство и заменив $b_1$ по формуле, получим: $c^2=a^2-2ab_1+b_1^2+b^2-b_1^2=a^2-2ab\cos{C}+b^2$.
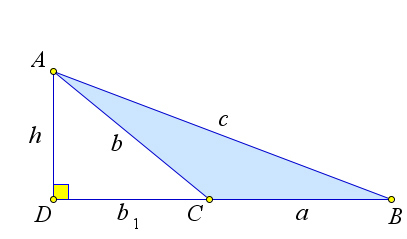
Третий случай.
Пусть $\a C>90^\circ$.
Снова проведем высоту $AD=h$ из вершины $A$.
Теперь ее основание – точка $D$ лежит на продолжении стороны $BC$ за точку $C$.
Снова обозначим отрезок $CD$ через $b_1$.
В этом случае $BD=a+b_1$ и из прямоугольного треугольника $ABD$ по теореме Пифагора $c^2=h^2+(a+b_1)^2$.
По определению косинуса тупого угла $\cos{C}=-\dfrac{b_1}{b}$.
Поэтому $b_1=-b\cos{C}$.
Наконец, из треугольника $ACD$ снова получаем, что $h^2=b^2-b_1^2$.
Подставляя это выражение для $h^2$ и выражение для $b_1$, то есть $b_1=-b\cos{C}$ в, снова получаем: $c^2=b^2-b_1^2+a^2+2ab_1+b_1^2=a^2+b^2-2ab\cos{C}$.
Второй способ.
Рассмотрим треугольник $ABC$ со сторонами $a,b$ и $c$.
Докажем, что $a^2=b^2+c^2-2bc\cos{A}$.
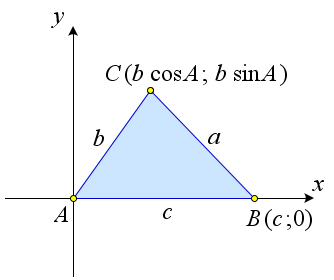
Введем систему координат с началом в точке $A$ так, чтобы $Ox\upuparrows \overrightarrow{AB}$, а точка $C$ имела бы положительную ординату.
Тогда точка $B$ имеет координаты $(c;0)$, а точка $C$ имеет координаты $(b\cos{A};b\sin{A})$.
По формуле расстояния между двумя точками получаем: $BC^2=a^2=(b\cos{A}-c)^2+b^2\sin^2{A}=b^2\cos^2{A}+b^2\sin^2{A}-2bc\cos{A}+c^2=b^2+c^2-2bc\cos{A}$.