Середины сторон произвольного четырехугольника являются вершинами параллелограмма.

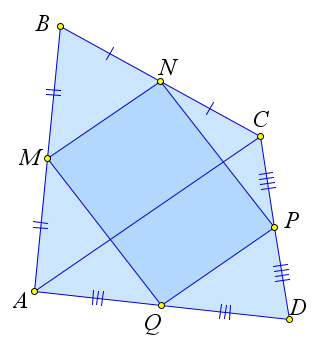
Рассмотрим произвольный четырехугольник $ABCD$, в котором точки $M,N,P$ и $Q$ являются серединами сторон $AB, BC, CD$ и $AD$ соответственно.

Докажем, что $MNPQ$ – параллелограмм

Действительно, $MN$ – средняя линия треугольника $ABC$, а $QP$ – средняя линия треугольника $ADC$.

Следовательно, $MN\parallel AC\parallel QP$ и $MN=\frac{1}{2}\cdot AC=QP$.

Тогда $MNPQ$ - параллелограмм по первому признаку.

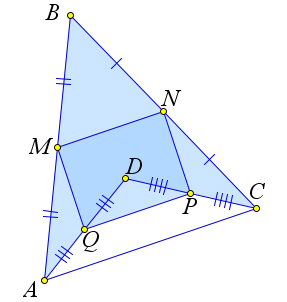
Доказательство не изменяется, если $ABCD$ – невыпуклый четырехугольник.