Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

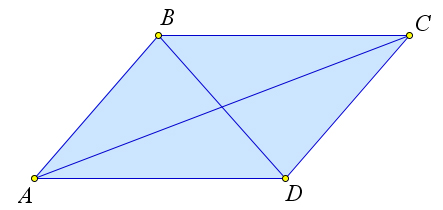
Рассмотрим параллелограмм $ABCD$.

Докажем, что $AC^2+BD^2=AB^2+BC^2+CD^2+AD^2$.

По теореме косинусов для треугольника $ABC$ имеем: $AC^2=AB^2+BC^2-2\cdot AB\cdot BC\cos{B}$.

По теореме косинусов для треугольника $BAD$ имеем: $BD^2=AB^2+AD^2-2\cdot AB\cdot AD\cos{A}$.

Но так как $ABCD$ – это параллелограмм, то $\angle A=180^\circ-\angle B, BC=AD$.

Следовательно, $\cos{A}=-\cos{B}$ и $BD^2=AB^2+BC^2+2\cdot AB\cdot BC\cos{B}$.

Складывая это равенство с выражением для $AC^2$ получим: $AC^2+BD^2=AB^2+BC^2+CD^2+AD^2$.