Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Рассмотрим треугольник $\triangle ABC$ с прямым углом $C$.

Пусть $AB=c, AC=b, BC=a$.

Докажем, что $a^2+b^2=c^2$.

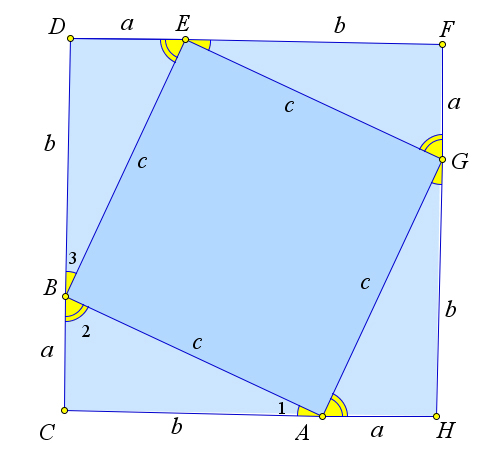
Достроим треугольник $ABC$ до квадрата $CDFH$ со стороной $(a+b)$ так, как это показано на рисунке.

Треугольники $\triangle ABC$, $\triangle BDE$, $\triangle EFG$ и $\triangle GHA$ равны по двум катетам.

Тогда у них равны гипотенузы, следовательно $EGAB$ – ромб.

Кроме того из равенства этих треугольников следует, что $\angle 1=\angle 3$, а так как $\angle 1+\angle 2=90^\circ$, то $\angle 2+\angle 3=90^\circ$, следовательно, $\angle ABE=90^\circ$, то есть $BEGA$ – ромб с прямым углом, то есть квадрат.

Квадрат $CDFH$ – составлен из четырех равных треугольников и квадрата со стороной $c$.

Тогда с одной стороны $S_{CDFH}=(a+b)^2$, а с другой $S_{CDFH}=4S_{ABC}+c^2$.

Следовательно, $(a+b)^2=4\cdot\dfrac{ab}{2}+c^2$, откуда $a^2+b^2=c^2$.

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Пусть в треугольнике $\triangle ABC$ выполняется равенство $AB^2=AC^2+BC^2$.

Докажем, что $\angle C=90^\circ$.

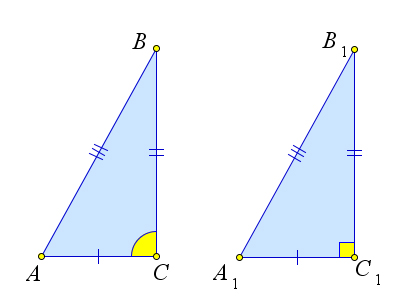
Рассмотрим прямоугольный треугольник $A_1B_1C_1$ с прямым углом $\angle C_1$, у которого $A_1C_1=AC$ и $B_1C_1=BC$.

По теореме Пифагора $A_1B_1^2=A_1C_1^2+B_1C_1^2$, и, значит, $A_1B_1^2=AC^2+BC^2=AB^2$, то есть $A_1B_1=AB$.

Тогда треугольники $ABC$ и $A_1B_1C_1$ равны по третьему признаку равенства, следовательно, $\angle C=\angle C_1=90^\circ.$

Площадь треугольника со сторонами $a,b$ и $c$ и полупериметром $p$ вычисляется по формуле $S=\sqrt{p(p-a)(p-b)(p-c)}$.

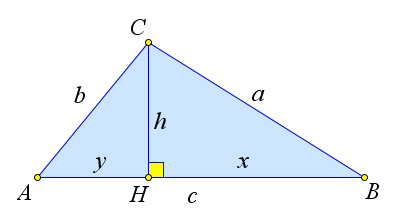
Рассмотрим треугольник $ABC$, в котором $AB=c, BC=a, AC=b$.

В любом треугольнике по крайней мере два угла острые.

Пусть $\angle A$ и $\angle B$ – острые углы треугольника $\triangle ABC$.

Тогда основание $H$ высоты $CH$ треугольника лежит на стороне $AB$.

Пусть $CH=h, AH=y, HB=x$.

По теореме Пифагора $a^2-x^2=h^2=b^2-y^2$, откуда $y^2-x^2=b^2-a^2$, или $(y-x)(y+x)=b^2-a^2$.

Так как $y+x=c$, то $y-x=\dfrac{b^2-a^2}{c}$.

Сложив два последних равенства и разделив на 2, получим: $y=\dfrac{b^2+c^2-a^2}{2c}$.

Поэтому

$h^2=b^2-y^2=(b+y)(b-y)=\left(b+\dfrac{b^2+c^2-a^2}{2c}\right)\left(b-\dfrac{b^2+c^2-a^2}{2c}\right)=\dfrac{(b+c)^2-a^2}{2c}\cdot\dfrac{a^2-(b-c)^2}{2c}=\dfrac{(b+c+a)(b+c-a)(a-b+c)(a+b-c)}{4c^2}=\dfrac{2p(2p-2a)(2p-2b)(2p-2c)}{4c^2}=\dfrac{4p(p-a)(p-b)(p-c)}{c^2}.$

Следовательно, $h=\dfrac{2\sqrt{p(p-a)(p-b)(p-c)}}{c}$.

Но $S_{ABC}=\dfrac{1}{2}hc=\sqrt{p(p-a)(p-b)(p-c)}$.