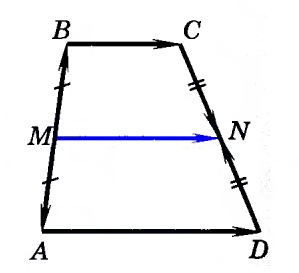
Теорема о средней линии трапеции
Теорема:
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть $MN$ - средняя линия трапеции $ABCD$.
Докажем, что $MN\parallel AD$ и $\frac{AD+BC}{2}=MN$.
По правилу многоугольника имеем:
- $\overrightarrow{MN} = \overrightarrow{MB} + \overrightarrow{BC} + \overrightarrow{CN}$
- $\overrightarrow{MN} = \overrightarrow{MA} + \overrightarrow{AD} + \overrightarrow{DN}$
Сложив эти равенства, получим:
$2\overrightarrow{MN} = \overrightarrow{MB} + \overrightarrow{MA} + \overrightarrow{BC} + \overrightarrow{AD} + \overrightarrow{CN}+\overrightarrow{DN}$.
Но $M$ и $N$ - середины сторон $AB$ и $CD$, поэтому
$\overrightarrow{MB} + \overrightarrow{MA} = \overrightarrow{0}$ и $\overrightarrow{CN} + \overrightarrow{DN} = \overrightarrow{0}$.
Следовательно, $2\overrightarrow{MN} = \overrightarrow{AD} + \overrightarrow{BC}$.
Откуда $\overrightarrow{MN} = \frac{\overrightarrow{AD} + \overrightarrow{BC}}{2}$.
Так как векторы $\overrightarrow{AD}$ и $\overrightarrow{BC}$ сонаправлены, то векторы $\overrightarrow{MN}$ и $\overrightarrow{AD}$ также сонаправлены, и $|\overrightarrow{AD} + \overrightarrow{BC}|=|AD|+|BC|$.
Отсюда следует, что $MN\parallel AD$ и $MN$ = $\frac{AD+BC}{2}$.