Если $\alpha$ – острый угол прямоугольного треугольника, то

1. $\sin^2{\alpha}+\cos^2{\alpha}=1$
2. $\tan^2{\alpha}+1=\dfrac{1}{\cos^2{\alpha}}$
3. 1. $\sin{(90^\circ-\alpha)}=\cos{\alpha}$
   2. $\cos{(90^\circ-\alpha)}=\sin{\alpha}$
   3. $\tan{(90^\circ-\alpha)}=\cot{\alpha}$

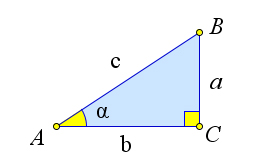
Рассмотрим прямоугольный треугольник $ABC$, в котором $\angle C=90^\circ, \angle A=\alpha, BC=a, AC=b, AB=c$.

Тогда

$\sin^2{\alpha}+\cos^2{\alpha}=\dfrac{a^2}{c^2}+\dfrac{b^2}{c^2}=\dfrac{a^2+b^2}{c^2}=\dfrac{c^2}{c^2}=1$.

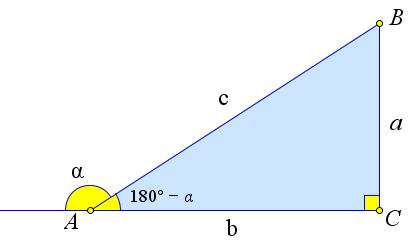
Если угол $\alpha$ тупой, то $\sin{\alpha}=\sin{(180^\circ-\alpha)}$ и $\cos{\alpha}=-\cos{(180^\circ-\alpha)}$.

А так как угол $180^\circ-\alpha$ – острый, то $1=\sin^2{(180^\circ-\alpha)}+\cos^2{(180^\circ-\alpha)}=\sin^2{\alpha}+(-\cos{\alpha})^2=\sin^2{\alpha}+\cos^2{\alpha}$.

$$\tan^2{\alpha}+1=\dfrac{\sin^2{\alpha}}{\cos^2{\alpha}}+1=\dfrac{\sin^2{\alpha}+\cos^2{\alpha}}{\cos^2{\alpha}}=\dfrac{1}{\cos^2{\alpha}}.$$

Рассмотрим прямоугольный треугольник $ABC$, в котором $\angle C=90^\circ, \angle A=\alpha, BC=a, AC=b, AB=c$. Тогда $\sin{(90^\circ-\alpha)}=\sin{B}=\dfrac{b}{c}=\cos{\alpha}$, $\cos{(90^\circ-\alpha)}=\cos{B}=\dfrac{a}{c}=\sin{\alpha}$, $\tan{(90^\circ-\alpha)}=\tan{B}=\dfrac{b}{a}=\cot{\alpha}$.

1. $\sin{30^\circ}=\dfrac{1}{2},\cos{30^\circ}=\dfrac{\sqrt{3}}{2}, \tan{30^\circ}=\dfrac{1}{\sqrt{3}}$.
2. $\sin{60^\circ}=\dfrac{\sqrt{3}}{2}$, $\cos{60^\circ}=\dfrac{1}{2}$, $\tan{60^\circ}=\sqrt{3}$
3. $\sin{45^\circ}=\dfrac{\sqrt{2}}{2}$, $\cos{45^\circ}=\dfrac{\sqrt{2}}{2}$, $\tan{45^\circ}=1$.

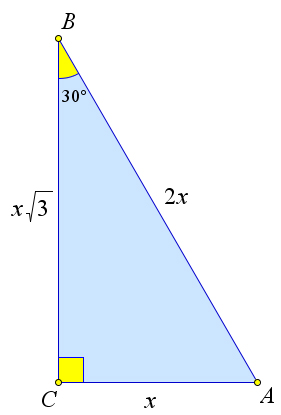
Рассмотрим прямоугольный треугольник $ABC$, в котором $\a B=30^\circ$.

Тогда катет $AC$ в два раза меньше гипотенузы $AB$: $AC=x, AB=2x$.

По теореме Пифагора $BC=\sqrt{4x^2-x^2}=x\sqrt{3}$.

Тогда

$\sin{B}=\sin{30^\circ}=\dfrac{x}{2x}=\dfrac{1}{2}$,

$\cos{B}=\cos{30^\circ}=\dfrac{x\sqrt{3}}{2x}=\dfrac{\sqrt{3}}{2}$,

$\tan{B}=\tan{30^\circ}=\dfrac{x}{x\sqrt{3}}=\dfrac{1}{\sqrt{3}}$,

$\cos{A}=\cos{60^\circ}=\dfrac{x\sqrt{3}}{2x}=\dfrac{\sqrt{3}}{2}$,

$\sin{A}=\sin{60^\circ}=\dfrac{x}{2x}=\dfrac{1}{2}$,

$\tan{A}=\tan{60^\circ}=\frac{x\sqrt{3}}{x}=\sqrt{3}$.

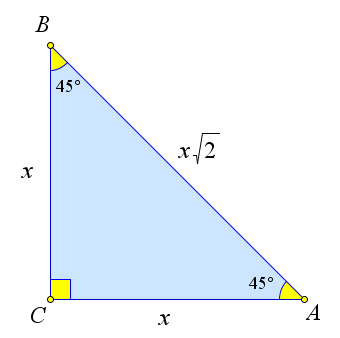
Рассмотрим прямоугольный треугольник $ABC$, в котором $\a C=90^\circ, \angle A=\angle B=45^\circ$.

Обозначим $BC=AC=x$, тогда по теореме Пифагора $AB=\sqrt{x^2+x^2}=x\sqrt{2}$.

Тогда $\sin{A}=\sin{45^\circ}=\dfrac{x}{x\sqrt{2}}=\cos{A}=\cos{45^\circ}$.