$\newcommand{\updownarrows}{\uparrow\!\downarrow}$ $\newcommand{\tg}{\mathop{\rm tg}\nolimits}$ $\newcommand{\ctg}{\mathop{\rm ctg}\nolimits}$ $\newcommand{\sign}{\mathop{\rm sign}\nolimits}$ $\newcommand{\arctg}{\mathop{\rm arctg}\nolimits}$ $\newcommand{\arcctg}{\mathop{\rm arcctg}\nolimits}$ $\newcommand{\deg}{^\circ}$ $\newcommand{\a}{\angle}$
Уравнение прямой с угловым коэффициентом
$y=kx+b$
Доказательство
Пусть прямая задана общим уравнением $Ax+By+C=0$, причём $A\neq0$ (коэффициенты $A,B$ и $C$ обозначены большими буквами, чтобы не было накладки обозначений).
Тогда можно выразить $y=-\frac{B}{A}x-\frac{C}{A}$.
Обозначив $k=-\frac{B}{A}, b=-\frac{C}{A}$, получим $y=kx+b$.
Теорема
Коэффициент $k$ в уравнение прямой с угловым коэффициентом равен тангенсу угла наклона прямой к оси $OX$.
Доказательство
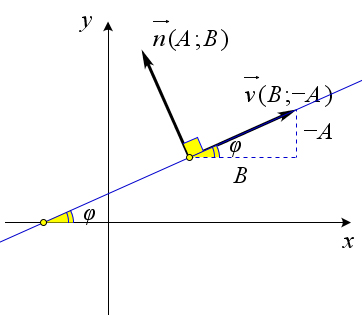
Из вывода уравнения прямой с угловым коэффициентом следует, что $k=-\frac{B}{A},$ где вектор нормали $\vec{n}$ к данной прямой имеет координаты $(A,B)$.
Тогда вектор $v(B;-A)$ будет направляющим вектором данной прямой, так как $n\cdot v=A\cdot B+B\cdot(-A)=0$.
Тангенс угла наклона направляющего вектора равен тангенсу угла наклона прямой, вне зависимости от выбора направляющего вектора, так как $\tg{(180^\circ-\varphi)}=\tg{\varphi}$.
Тангенс угла наклона вектора $v(B;-A)$ очевидно равен $\tg{\varphi}=\frac{-A}{B}=-\frac{A}{B}$.