$\overrightarrow{OX}=\overrightarrow{OA}+t\cdot\overrightarrow{AB}$, где $X$ – переменная точка прямой $AB$.

рис. 1a	рис. 1b	рис. 1c

Пусть $X$ – произвольная точка прямой $AB$.

Тогда вектора $\overrightarrow{AX}$ и $\overrightarrow{AB}$ коллинеарны, и, следовательно существует такое число $t$, что $\overrightarrow{AX}=t\cdot \overrightarrow{AB}$.

Тогда, взяв произвольную точку $O$, можно написать $\overrightarrow{OX}=\overrightarrow{OA}+\overrightarrow{AX}=\overrightarrow{OA}+t\cdot \overrightarrow{AB}$.

Таким образом для произвольной точки $X$ прямой $AB$ можно написать уравнение $\overrightarrow{OX}=\overrightarrow{OA}+t\cdot\overrightarrow{AB}$.

При этом очевидно, что для каждого числа $t$ существует единственная точка $X$, для которой равенство будет верно, и наоборот.

$\overrightarrow{OX}=(1-t)\cdot \overrightarrow{OA}+t\cdot\overrightarrow{OB}$, где $X$ – переменная точка прямой $AB$, причем

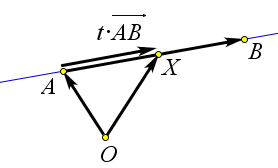
1. $X$ лежит между точками $A$ и $B$, если $0<t<1$
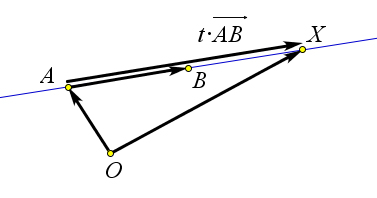
2. $X$ лежит за точкой $B$, если $t>1$
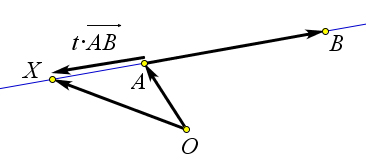
3. $X$ лежит за точкой $A$, если $t<0$
4. $X$ совпадает с точкой $A$, если $t=0$
5. $X$ совпадает с точкой $B$, если $t=1$.

Преобразуем правую часть данного уравнения: $\overrightarrow{OX}=(1-t)\cdot \overrightarrow{OA}+t\cdot \overrightarrow{OB}=\overrightarrow{OA}+t\cdot(\overrightarrow{OB}-\overrightarrow{OA})=\overrightarrow{OA}+t\cdot \overrightarrow{AB}$.

То есть $\overrightarrow{OX}=\overrightarrow{OA}+t\cdot \overrightarrow{AB}$.

Тогда, перенеся вектор $\overrightarrow{OA}$ в правую часть и преобразовав разность по правилу треугольника, получим $\overrightarrow{AX}=t\cdot \overrightarrow{AB}$.

Откуда в силу определения умножения вектора на число ясно, что точка $X$ лежит между точками $A$ и $B$, если $0<t<1$, лежит за точкой $B$, если $t>1$, лежит за точкой $A$, если $t<0$, совпадает с точкой $A$, если $t=0$, совпадает с точкой $B$, если $t=1$.