Содержание
Направленные отрезки
Определение
Направленный отрезок – это отрезок, одна граничная точка которого считается «началом», а другая – «концом».
Определение
Длиной направленного отрезка $[\overrightarrow{AB}]$ называется длина отрезка $AB$.
Определение
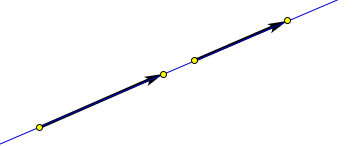
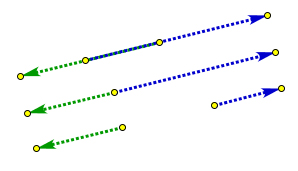
Направленные отрезки называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Определение
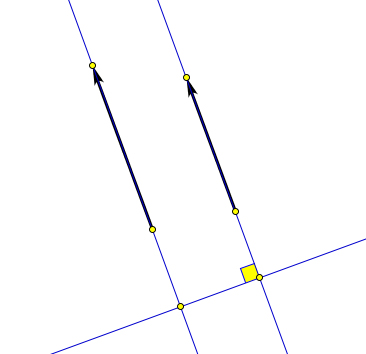
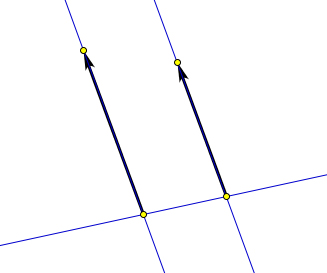
Направленные отрезки $[\overrightarrow{AB}]$ и $[\overrightarrow{CD}]$ сонаправлены, если найдётся такая прямая $a$, что, во-первых, они перпендикулярны этой прямой и, во-вторых, лучи $AB$ и $CD$ лежат по одну сторону от этой прямой.
Определение
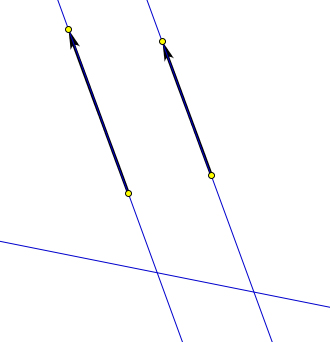
Направленные отрезки называются противоположно направленными, если они лежат на параллельных прямых (или на одной прямой), но не сонаправлены.
Теорема
Доказательство
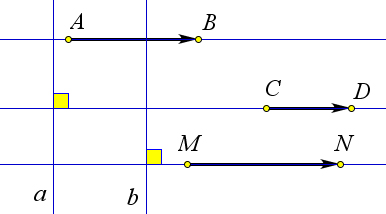
Пусть $[\overrightarrow{AB}]$ и $[\overrightarrow{CD}]$ сонаправлены с $[\overrightarrow{MN}]$.
Докажем, что $[\overrightarrow{AB}]\upuparrows [\overrightarrow{CD}]$.
Так как $[\overrightarrow{AB}]\upuparrows [\overrightarrow{MN}]$, то по определению найдется такая перпендикулярная им прямая $a$, от которой лучи $AB$ и $MN$ лежат по одну сторону.
Точно так же для $[\overrightarrow{CD}]$ и $[\overrightarrow{MN}]$ найдётся перпендикулярная им прямая $b$, от которой лучи $CD$ и $MN$ лежат по одну сторону.
Если прямые $a$ и $b$ не совпадают, то они параллельны (как перпендикулярные одной и той же прямой $MN$).
Тогда из двух полуплоскостей, которые ограничены прямыми $a$ и $b$ и содержат луч $MN$, одна содержит другую.
Будем считать, что это полуплоскость ограниченная прямой $a$.
Эта полуплоскость содержит лучи $AB$, $CD$ и $MN$.
Тем самым выполнено второе условие определения.
Кроме того выполнено и первое условие, так как $[\overrightarrow{AB}]$ и $[\overrightarrow{CD}]$ перпендикулярны прямой $a$.
Поэтому $[\overrightarrow{AB}]\upuparrows [\overrightarrow{CD}]$.
Определение
Направленные отрезки называются равными, если они равны по длине и сонаправлены.