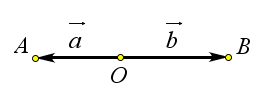Скалярное умножение векторов

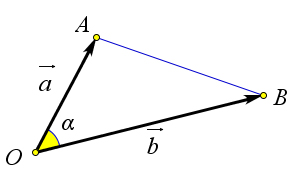
Углом между двумя ненулевыми векторами называется величина образуемого ими угла, когда они отложены от одной точки.

Скалярным произведением двух векторов называется произведение их модулей и косинуса угла между ними. Если хотя бы один из векторов нулевой, то их скалярное произведение полагают равным нулю.

Скалярным квадратом вектора называется его произведение самого на себя.

Для любых двух ненулевых векторов их скалярное произведение равно нулю тогда и только тогда, когда они перпендикулярны.

Пусть $\alpha=\angle (\vec{a};\vec{b})$.

Если $\alpha=90^\circ$, то $\cos{\alpha}=0$, следовательно $\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos{\alpha}=0$.

Если $\vec{a}\cdot \vec{b}=0$, то $|\vec{a}||\vec{b}|\cos{\alpha}=0$.

Но поскольку $|\vec{a}|\neq0$ и $|\vec{b}|\neq 0$ по условию, то $\cos{\alpha}=0$.

А значит, $\alpha=90^\circ$.

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат.

Если хотя бы один из векторов $\vec{a}$ или $\vec{b}$ нулевой, то справедливость теоремы очевидна.

Рассмотрим случай, когда векторы $\vec{a}$ и $\vec{b}$ ненулевые.

Отложим от произвольной точки $O$ векторы $\overrightarrow{OA}=\vec{a}$ и $\overrightarrow{OB}=\vec{b}$.

Пусть $\alpha=\angle (\vec{a};\vec{b})$.

Если векторы $\vec{a}$ и $\vec{b}$ не коллинеарны, то по теореме косинусов $AB^2=OA^2+OB^2-2OA\cdot OB\cos{\alpha}$.

Это равенство верно и в том случае, если векторы $\vec{a}$ и $\vec{b}$ коллинеарны.

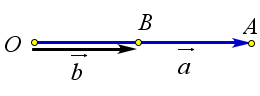
Действительно, если $\vec{a}\upuparrows \vec{b}$, то $AB^2=(OA-OB)^2=OA^2+OB^2-2OA\cdot OB=OA^2+OB^2-2OA\cdot OB\cos{0^\circ}=OA^2+OB^2-2OA\cdot OB\cos{\alpha}$.

Если же $a\updownarrows b$, то $AB^2=(OA+OB)^2=OA^2+OB^2+2OA\cdot OB=OA^2+OB^2-2OA\cdot OB\cos{180^\circ}=OA^2+OB^2-2OA\cdot OB\cos{\alpha}$.

Так как $\overrightarrow{AB}=\vec{b}-\vec{a}, \overrightarrow{OA}=\vec{a}, \overrightarrow{OB}=\vec{b}$, то равенство \eqref{eq008} можно записать так: $|\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}^2|-2\vec{a}\cdot \vec{b}$.

Откуда $\vec{a}\cdot\vec{b}=\frac{1}{2}(|\vec{a}|^2+|\vec{b}|^2-|\vec{a}-\vec{b}|^2)$.

Векторы $\vec{a}, \vec{b}$ и $\vec{b}-\vec{a}$ имеют координаты $(x_1; y_1), (x_2; y_2)$ и $(x_2-x_1; y_2-y_1)$.

Поэтому $|\vec{a}|^2=x_1^2+y_1^2, |\vec{b}|^2=x_2^2+y_2^2, |\vec{b}-\vec{a}|^2=(x_2-x_1)^2+(y_2-y_1)^2$.

Подставив эти выражения в правую часть равенства \eqref{eq009}, получим $\vec{a}\cdot \vec{b}=\frac{1}{2}\left(x_1^2+y_1^2+x_2^2+y_2^2-x_1^2-x_2^2+2x_1x_2-y_1^2-y_2^2+2y_1y_2\right)=x_1x_2+y_1y_2$.

1. $\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a}$;
2. $(k\vec{a})\cdot \vec{b}=k(\vec{a}\cdot \vec{b})$;
3. $(\vec{a}+\vec{b})\cdot \vec{c}=\vec{a}\cdot \vec{c}+\vec{b}\cdot \vec{c}$.

Первое свойство очевидно в силу определения скалярного произведения.

Действительно, $\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos{\angle (\vec{a};\vec{b})}=|\vec{b}||\vec{a}|\cos{\angle (\vec{b};\vec{a})}=\vec{b}\cdot \vec{a}$.

Докажем второе свойство, используя теорему \ref{149}.

Пусть $\vec{a}$ имеет координаты $(x_1;y_1)$, а вектор $\vec{b}$ имеет координаты $(x_2;y_2)$.

Тогда вектор $(k\vec{a})\cdot\vec{b}=kx_1;ky_1)\cdot(x_2;y_2)=kx_1x_2+ky_1y_2=k(x_1x_2+y_1y_2)=k\vec{a}\cdot\vec{b}$.

Докажем третье свойство, используя теорему \ref{149}.

Пусть вектор $a$ имеет координаты $(x_a;y_a)$, вектор $b$ имеет координаты $(x_b;y_b)$, вектор $c$ имеет координаты $(x_c;y_c)$.

Тогда $(\vec{a}+\vec{b})\cdot \vec{c}=(x_a+x_b;y_a+y_b)\cdot(x_c;y_c)=(x_a+x_b)x_c+(y_a+y_b)y_c=\\=x_ax_c+x_bx_c+y_ay_c+y_by_c=(x_ax_c+y_ay_c)+(x_bx_c+y_by_c)=\vec{a}\cdot\vec{c}+\vec{b}\cdot \vec{c}$.

1. $|\vec{a}|=\sqrt{\vec{a}^2}$;
2. $\cos{\angle(\vec{a};\vec{b})}=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$;
3. $pr_{\vec{a}}(\vec{b})=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}|}$