Линейные операции с векторами

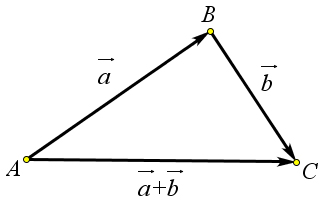
Чтобы получить сумму векторов $\vec{a}$ и $\vec{b}$, нужно от какой-либо точки $A$ отложить вектор $\overrightarrow{AB}=\vec{a}$, затем от точки $B$ отложить вектор $\overrightarrow{BC}=\vec{b}$.

Вектор $\overrightarrow{AC}$ называется суммой векторов $\vec{a}$ и $\vec{b}$.

$\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

Суммой двух векторов называется вектор, полученный по правилу треугольника.

Определение суммы векторов корректно, то есть сумма векторов не зависит от выбора точки $A$.

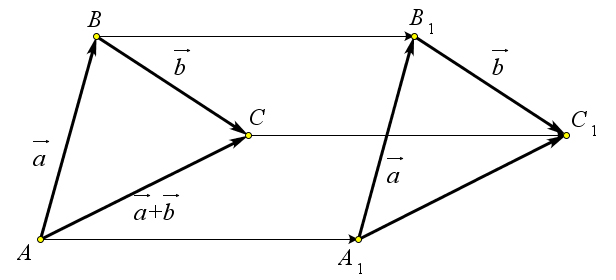
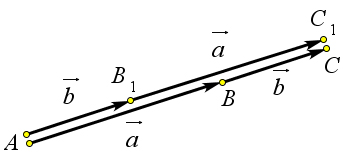
Докажем, что если отложить вектор $a$ от точки $A_1$, то есть $\overrightarrow{A_1B_1}=\vec{a}$, а затем от точки $B_1$ отложить вектор $\overrightarrow{B_1C_1}=\vec{b}$, то сумма векторов $\overrightarrow{A_1B_1}+\overrightarrow{B_1C_1}=\overrightarrow{A_1C_1}$ будет равна вектору $\overrightarrow{AC}$, то есть $\overrightarrow{A_1C_1}=\overrightarrow{AC}$ (рис. \ref{pic133}).

Так как $\overrightarrow{AB}=\overrightarrow{A_1B_1}$, то по теореме \ref{133} имеем $\overrightarrow{AA_1}=\overrightarrow{BB_1}$.

Аналогично из равенства $\overrightarrow{B_1C_1}=\overrightarrow{BC}$ следует, что $\overrightarrow{BB_1}=\overrightarrow{CC_1}$.

Поэтому $\overrightarrow{AA_1}=\overrightarrow{CC_1}$.

Но из этого равенства по той же теореме \ref{133} следует, что $\overrightarrow{A_1C_1}=\overrightarrow{AC}$.

Если $ABCD$ – параллелограмм, то $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$

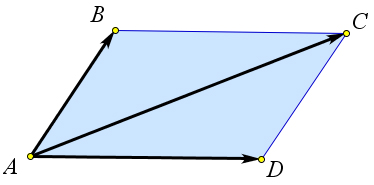
Так как $ABCD$ – параллелограмм, то $\overrightarrow{AD}=\overrightarrow{BC}$. Следовательно, $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

Для любых векторов $\vec{a}, \vec{b}$ и $\vec{c}$

1. $\vec{a}+\vec{0}=\vec{a}$.
2. $\vec{a}+\vec{b}=\vec{b}+\vec{a}$.
3. $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$.

Первой свойство очевидно.

Докажем второе свойство.

Возможны два случая: $1)$ векторы $\vec{a}$ и $\vec{b}$ неколлинеарны, 2) вектора $\vec{a}$ и $\vec{b}$ коллинеарны.

Рассмотрим первый случай.

Пусть вектора $\vec{a}$ и $\vec{b}$ неколлинеарны.

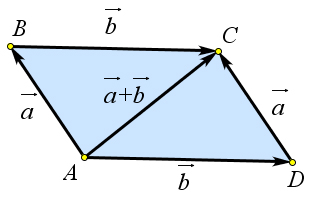
Отложим их от точки $A$: $\overrightarrow{AB}=a$ и $\overrightarrow{AD}=b$ – и построим на этих векторах параллелограмм $ABCD$ (рис. \ref{pic136} a).

Поскольку $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}, \overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}, \overrightarrow{AB}=\overrightarrow{DC}=\vec{a}$ и $\overrightarrow{BC}=\overrightarrow{AD}=\vec{b}$, то $\vec{a}+\vec{b}=\vec{b}+\vec{a}$.

Рассмотрим второй случай.

Пусть вектора $\vec{a}$ и $\vec{b}$ коллинеарны.

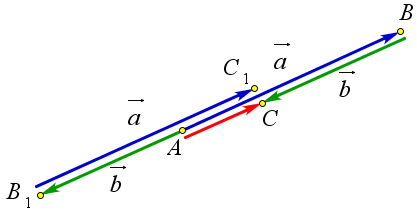
Если вектора $\vec{a}$ и $\vec{b}$ сонаправлены, то можно их последовательно отложить от точки $A$ двумя способами, то есть $\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, или $\vec{b}+\vec{a}=\overrightarrow{AB_1}+\overrightarrow{B_1C_1}=\overrightarrow{AC_1}$ (рис. \ref{pic136} b).

Докажем, что $\overrightarrow{AC}=\overrightarrow{AC_1}$.

Вектора $\overrightarrow{AC}$ и $\overrightarrow{AC_1}$ очевидно сонаправлены, кроме того их модули равны $|\vec{a}|+|\vec{b}|$.

Следовательно, эти вектора равны.

Рассмотрим случай, когда вектора $\vec{a}$ и $\vec{b}$ противоположно направлены (рис. \ref{pic136} c).

Пусть кроме того $|\vec{a}|>|\vec{b}|$.

Тогда $\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, при этом $|\overrightarrow{AC}|=|\vec{a}|-|\vec{b}|$.

C другой стороны $\vec{b}+\vec{a}=\overrightarrow{AB_1}+\overrightarrow{B_1C_1}=\overrightarrow{AC_1}$, при этом $|\overrightarrow{AC_1}|=|\vec{a}|-|\vec{b}|$.

Таким образом модули векторов $\overrightarrow{AC}$ и $\overrightarrow{AC_1}$ равны, кроме того они сонаправлены, следовательно, $\overrightarrow{AC}=\overrightarrow{AC_1}$.

Докажем третий пункт теоремы.

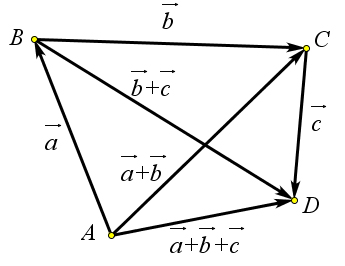
Отложим от точки $A$ вектор $\overrightarrow{AB}=\vec{a}$, затем от точки $B$ вектор $\overrightarrow{BC}=\vec{b}$, а потом от точки $C$ вектор $\overrightarrow{CD}=\vec{c}$ (рис. \ref{pic136} d).

Тогда $(\vec{a}+\vec{b})+\vec{c}=(\overrightarrow{AB}+\overrightarrow{BC})+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}$.

C другой стороны, $\vec{a}+(\vec{b}+\vec{c})=\overrightarrow{AB}+(\overrightarrow{BC}+\overrightarrow{CD})=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}$. Итак $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$.

При любом расположении точек $A_1, A_2, A_3, \ldots, A_n$ верно равенство $\overrightarrow{A_1A_2}+\overrightarrow{A_2A_3}+\ldots+\overrightarrow{A_{n-1}A_n}=\overrightarrow{A_1A_n}$

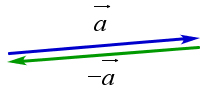
Два ненулевых вектора называются противоположными, если их длины равны и они противоположны по направлению. Ноль-вектор считается противоположным самому себе (рис. \ref{pic137}).

1. $\vec{a}+(-\vec{a})=\vec{0}$.
2. Если $\vec{a}+\vec{b}=\vec{0}$, то $\vec{a}=-\vec{b}$.

Докажем первый пункт.

Пусть $\vec{a}=\overrightarrow{AB}$.

Тогда $-\vec{a}=\overrightarrow{BA}$.

Следовательно, $\vec{a}+(-\vec{a})=\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow{AA}=\vec{0}$.

Докажем второй пункт.

Пусть $\vec{a}+\vec{b}=\vec{0}$.

Тогда, если $\vec{a}=\overrightarrow{AB}$, то поскольку $\vec{0}=\overrightarrow{AA}$, то $\vec{b}=\overrightarrow{BA}$.

Таким образом, вектора $\vec{a}$ и $\vec{b}$ равны по модулю и противоположны по направлению, то есть векторы $\vec{a}$ и $\vec{b}$ противоположны.

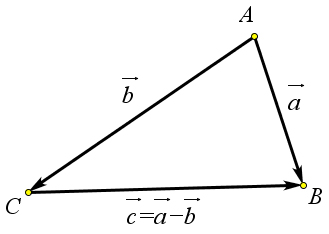
Разностью векторов $\vec{a}$ и $\vec{b}$ называется такой вектор $\vec{c}$, что $\vec{c}+\vec{b}=\vec{a}$. Принято обозначать $\vec{c}=\vec{a}-\vec{b}$.

$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$.

Для любых двух векторов $\vec{a}$ и $\vec{b}$ справедливо равенство $\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$.

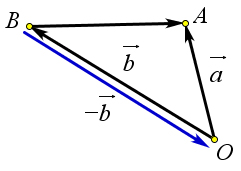
Пусть $\vec{c}=\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}=\vec{a}-\vec{b}$.

По правилу треугольника $\overrightarrow{BA}=\overrightarrow{BO}+\overrightarrow{OA}$.

Кроме того $\overrightarrow{BO}=-\overrightarrow{OB}=-\vec{b}$.

Поэтому $\vec{a}- \vec{b}=\overrightarrow{BA}=\overrightarrow{BO}+\overrightarrow{OA}=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{OA}+(-\overrightarrow{OB})=\vec{a}+(-\vec{b})$.