Для любых чисел $k, l$ и любых векторов $\vec{a}, \vec{b}$ справедливы равенства:

1. $(kl)\vec{a}=k(l\vec{a})$;
2. $k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$.
3. $(k+l)\vec{a}=k\vec{a}+l\vec{a}$;

Докажем, что для любых чисел $k$, $l$ и любого вектора $\vec{a}$ справедливо равенство $(kl)\vec{a}=k(l\vec{a})$.

Если $\vec{a}=\vec{0}$, то справедливость этого равенство очевидна.

Пусть $\vec{a}\neq\vec{0}$.

Имеем: $|(lk)\vec{a}|=|kl|\cdot|\vec{a}|=|k|\cdot|l|\cdot|\vec{a}|=|k|\cdot|l\vec{a}|=|k(l\vec{a})|$.

Далее, если $k\cdot l\geqslant0$, то $(kl)\vec{a}\upuparrows \vec{a}$ и $k(l\vec{a})\upuparrows \vec{a}$.

Если же $k\cdot l<0$, то $(kl)\vec{a}\updownarrows \vec{a}$ и $k(l\vec{a})\updownarrows \vec{a}$.

И в том и в другом случае $(kl)\vec{a}\upuparrows k(l\vec{a})$.

Следовательно, $(kl)\vec{a}=k(l\vec{a})$.

Докажем, что для любого числа $k$ и любых векторов $\vec{a}$ и $\vec{b}$ справедливо равенство $k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$.

Если $k=0$, или $\vec{a}=\vec{0}$, или $\vec{b}=\vec{0}$, то справедливость этого равенства очевидна.

Пусть $k\neq0, \vec{a}\neq\vec{0}, \vec{b}\neq\vec{0}.$

Возможны три случая.

Пусть $\vec{a}\upuparrows \vec{b}$.

Тогда вектора $k(\vec{a}+\vec{b}), k\vec{a}$, $k\vec{b}$, а следовательно, и $k\vec{a}+k\vec{b}$, сонаправлены.

Кроме того $|k(\vec{a}+\vec{b})|=|k|(|\vec{a}|+|\vec{b}|)=|k\vec{a}|+|k\vec{b}|=|k\vec{a}+k\vec{b}|$.

Следовательно, $k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$.

Пусть $\vec{a}\updownarrows \vec{b}$.

Пусть для определённости $|\vec{a}|\geqslant|\vec{b}|$.

Тогда и $|k\vec{a}|\geqslant|k\vec{b}|$.

Тогда $k(\vec{a}+\vec{b})\upuparrows(k\vec{a}+k\vec{b})$.

Кроме того в этом случае $|k(\vec{a}+\vec{b})|=|k|(|\vec{a}|-|\vec{b}|)=|k\vec{a}|-|k\vec{b}|=|k\vec{a}+k\vec{b}|$.

Следовательно, $k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$.

Пусть $\vec{a}\not \parallel \vec{b}$.

Тогда отложим от какой-нибудь точки $O$ векторы $\overrightarrow{OA_1}=\vec{a}$ и $\overrightarrow{OA}=k\vec{a}$, а от точек $A_1$ и $A$ векторы $\overrightarrow{A_1B_1}=\vec{b}$ и $\overrightarrow{AB}=k\vec{b}$.

Треугольники $OA_1B_1$ и $OAB$ подобны с коэффициентом подобия $|k|$ по второму признаку подобия треугольников.

Следовательно, $\overrightarrow{OB}=k\cdot \overrightarrow{OB_1}=k(\vec{a}+\vec{b})$.

C другой стороны, $\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}=k\vec{a}+k\vec{b}$.

Итак, $k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$.

Докажем, что для любых чисел $k, l$ и любого вектора $\vec{a}$ справедливо равенство $(k+l)\vec{a}=k\vec{a}+l\vec{a}$.

Если $k=l=0$, то справедливость этого равенство очевидна.

Пусть хотя бы одно из чисел $k, l$ отлично от нуля.

Для определённости будем считать, что $|k|\geqslant|l|$, и, следовательно, $k\neq0$ и $\left|\dfrac{l}{k}\right|\leqslant1$.

Рассмотрим вектор $\vec{a}+\dfrac{l}{k}\vec{a}$.

Очевидно, $(\vec{a}+\dfrac{l}{k}\vec{a})\upuparrows\vec{a}$.

Далее, $|\vec{a}+\dfrac{l}{k}\vec{a}|=|\vec{a}|+\dfrac{l}{k}|\vec{a}|=(1+\dfrac{l}{k})|\vec{a}|$.

Умножая обе части этого равенства на $k$, получим, что справедливо равенство $k\vec{a}+l\vec{a}=(k+l)\vec{a}$.

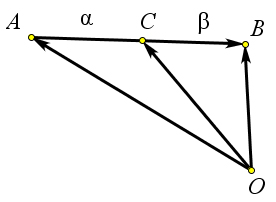
Если точка $C$ лежит на отрезке $AB$, и $AC:CB=\alpha:\beta$, то $\overrightarrow{OC}=\dfrac{\alpha}{\alpha+\beta}\,\overrightarrow{OB}+\dfrac{\beta}{\alpha+\beta}\,\overrightarrow{OA}$.

Выберем произвольную точку $O$ и обозначим $\vec{a}=\overrightarrow{OA}, \vec{b}=\overrightarrow{OB}, \vec{c}=\overrightarrow{OC}$.

Тогда $\overrightarrow{AB}=\vec{b}-\vec{a}$, $\displaystyle\overrightarrow{AC}=\frac{\alpha}{\alpha+\beta}\overrightarrow{AB}=\frac{\alpha}{\alpha+\beta}(\vec{b}-\vec{a})$.

Тогда
$\displaystyle\vec{c}=\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}=\vec{a}+\dfrac{\alpha}{\alpha+\beta}(\vec{b}-\vec{a})= \dfrac{\alpha \vec{a}+\beta \vec{a}+\alpha \vec{b}-\alpha\vec{a}}{\alpha+\beta}=\dfrac{\beta \vec{a}+\alpha\vec{b}}{\alpha+\beta}$

То есть $\vec{c}=\dfrac{\beta}{\alpha+\beta}\vec{a}+\dfrac{\alpha}{\alpha+\beta} \vec{b}$

Таким образом $\displaystyle\overrightarrow{OC}=\frac{\alpha}{\alpha+\beta}\,\overrightarrow{OB}+\frac{\beta}{\alpha+\beta}\,\overrightarrow{OA}$.

Если в треугольника $ABC$ $AM$ – это медиана, то $\overrightarrow{AM}=\dfrac{\overrightarrow{AB}+\overrightarrow{AB}}{2}$.