Осевая симметрия

Осевой симметрией относительно прямой $l$ называется такое преобразование плоскости, при котором точки прямой $l$ остаются неподвижными, а для любой точки $A$ не лежащей на прямой $l$ будет выполнено: $AA'\perp l$, $\rho(A; l)=\rho(A';l)$, где $A'$ – это образ точки $A$.

1. Образ точки $X(x_0;y_0)$ при осевой симметрии относительно прямой $l_1: y=a$ имеет координаты $X'(x_0;2a-y_0)$;
2. Образ точки $X(x_0;y_0)$ при осевой симметрии относительно прямой $l_2: x=b$ имеет координаты $X'(2b-x_0;y_0)$;
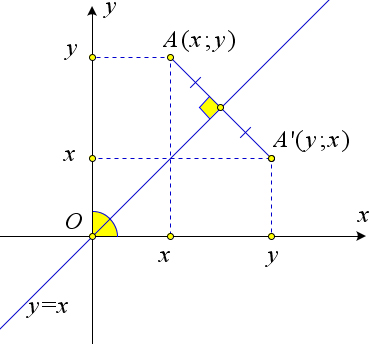
3. Образ точки $X(x_0;y_0)$ при осевой симметрии относительно прямой $l_3: x=y$ имеет координаты $X'(y_0;x_0)$.
4. Образ точки $X(x_0;y_0)$ при осевой симметрии относительно прямой $l_4: ax+by+c=0$ имеет координаты $X'\left(\dfrac{(b^2-a^2)x_0-2aby_0-2ac}{a^2+b^2};\dfrac{(a^2-b^2)y_0-2abx_0-2bc}{a^2+b^2}\right)$.

Пусть $X'=S_{l_1}(X)$.

Обозначим координаты точки $X'(x';y')$.

Очевидно, что $y'=y$.

Рассмотрим различные случаи расположения точки $X$ относительно прямой $l_1$.

Пусть $x_0>b$.

Тогда $x'=b-AX=b-(x_0-b)=2b-x_0$.

Если $x_0=b$, то $x'=x_0=2b-x_0$, то есть соотношение остаётся верным.

Если же $x_0<b$, то $x'=b+AX=b+(b-x_0)=2b-x_0$.

Пусть $X'=S_{l_2}(X)$.

Обозначим координаты точки $X'(x';y')$.

Очевидно, что $x'=x$.

Рассмотрим различные случаи расположения точки $X$ относительно прямой $l_2$.

Пусть $y_0>a$.

Тогда $y'=a-AX=a-(y_0-a)=2a-y_0$.

Если $y_0=a$, то $y'=y_0=2a-y_0$, то есть соотношение остаётся верным.

Если же $y_0<a$, то $y'=a+AX=a+(a-y_0)=2a-y_0$.

Прямая $l_3$ образует равные углы с осями координат.

А так как движение сохраняет углы, а точка $O$ остаётся неподвижной при осевой симметрии относительно прямой $l_3$, то образом оси абсцисс при осевой симметрии $S_{l_3}$ является ось ординат, и наоборот.

Следовательно, координаты точки при осевой симметрии $S_{l_3}$ меняются местами, то есть образом точки $X(x;y)$ будет являться точка $X'(y;x)$.

Осевая симметрия является движением..

Рассмотрим осевую симметрию $S_{l}$.

Докажем, что $S_{l}$ – это движение.

Введем систему координат таким образом, чтобы прямая $l$ совпадала с осью абсцисс.

Возьмём любые две точки $A(x_1, y_1)$ и $B(x_2,y_2)$ и рассмотрим симметричные им относительно оси $x$ точки $A'(x_1, -y_1)$ и $B'(x_2,-y_2)$.

По формуле расстояния между двумя точками

$$A'B'=\sqrt{(x_2-x_1)^2+(-y_2+y_1)^2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=AB.$$

Таким образом, осевая симметрия сохраняет расстояния, то есть является движением.

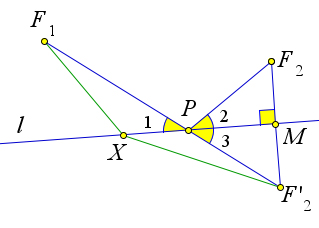
Пусть точки $F_1$ и $F_2$ лежат по одну сторону от прямой $l$. Сумма расстояний $F_1P+PF_2$, где точка $P$ лежит на прямой будет наименьшей, если лучи $PF_1$ и $PF_2$ образуют равные углы с прямой $l$.

Пусть $F'_2=S_{l}(F_2)$.

Пусть прямая $F_1F'_2$ пересекает прямую $l$ в точке $P$.

Тогда, так как $PF_2=PF'_2$, то $F_1P+PF_2=F_1P+PF'_2$.

Для любой точки $X$ прямой $l$, отличной от точки $P$, с учётом неравенства треугольника будет верно $F_1X+XF'_2=F_1X+XF'_2>F_1F'_2=F_1F_2$.

Таким образом сумма $F_1P+PF_2$ будет наименьшей.

Докажем теперь, что $\angle 1=\angle 2$.

Действительно, треугольник $F_2PF'_2$ равнобедренный, и, следовательно, высота $PM$ является биссектрисой.

Тогда $\angle 2=\angle 3$. Но $\angle 1=\angle 3$, как вертикальные. Следовательно, $\angle 1=\angle 2$.