Вневписанные окружности

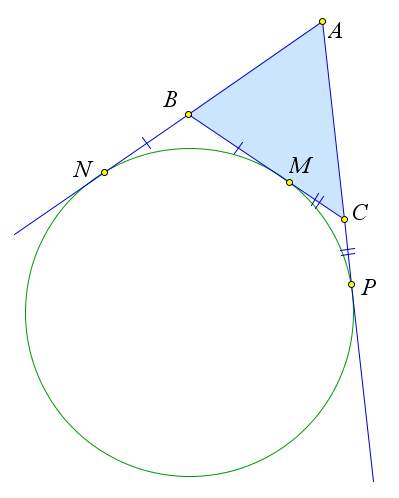
Окружность, касающаяся стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью этого треугольника.

У любого треугольника есть три вневписанных окружности.

Рассмотрим треугольник $ABC$.

Пусть биссектрисы внешних углов при вершинах $B$ и $C$ пересекаются в точке $O_a$.

Тогда точка $O_a$ равноудалена от прямых $AB, BC$ и $AC$.

Следовательно, точка $O_a$ лежит на биссектрисе угла $A$.

Обозначим расстояние от точки $O_a$ до стороны $BC$ за $r_a$.

Тогда окружность с центром в точке $O_a$ и радиусом $r_a$ касается стороны $BC$ и продолжений сторон $AB$ и $AC$, то есть является вневписанной окружностью данного треугольника.

Аналогично можно построить вневписанные окружности с центрами в точках $O_b$ и $O_c$, касающиеся сторон $AC$ и $BA$ соответственно.

Пусть в треугольнике $ABC$ биссектриса $AA_1$ пересекается с окружностью, описанной около этого треугольника, в точке $D$. Тогда точка $D$ является центром окружности, описанной около четырёхугольника $BOCO_a$, где $O$ – центр окружности, вписанной в треугольник $ABC$, а $O_a$ – центр вневписанной окружности.

Точка $O$, как центр окружности, вписанной в треугольник $ABC$, лежит на биссектрисе угла $B$, а точка $O_a$, как центр вневписанной окружности лежит на биссектрисе угла, смежного с углом $B$.

Вспомним, что биссектрисы смежных углов перпендикулярны.

Следовательно $\angle OBO_a=90^\circ$. Аналогично $\angle OCO_a=90^\circ$.

Следовательно, около четырёхугольника $BOCO_a$ можно описать окружность.

Пусть продолжение биссектрисы $AA_1$ и $BB_1$ пересекают окружность, описанную около треугольника $ABC$ в точке $D$ и $E$.

Так как $AD$ и $BE$ – биссектрисы, то $\buildrel\,\,\frown\over{BD}=\buildrel\,\,\frown\over{DC}, \buildrel\,\,\frown\over{AE}=\buildrel\,\,\frown\over{EC}$.

Обозначим эти пары углов соответственно $\alpha$ и $\beta$.

Тогда $\angle EBD=\frac{\alpha+\beta}{2}$, так как он вписанный, а $\angle BOD=\frac{\alpha+\beta}{2}$.

Следовательно, в треугольнике $BOD$ углы при основании $BOD$ равны, то есть он равнобедренный $BD=DO$.

Таким образом $BD=DO=DC$.

Таким образом точка $D$ равноудалена от всех вершин треугольник $BOC$, и, следовательно, является центром окружности, описанной около этого треугольника.

Но эта окружность является также окружностью, описанной около четырёхугольника $BOCO_a$.

Точки, в которых вписанная и вневписанная окружности касаются стороны треугольника, симметричны относительно середины этой стороны.

Рассмотрим треугольник $ABC$.

Пусть вневписанная окружность $\omega_a(O_a,r_a)$ и вписанная окружность $\omega(O,r)$ касаются стороны $BC$ в точках $P$ и $Q$.

Докажем, что точки $P$ и $Q$ симметричны относительно точки $M$ – середины стороны $BC$.

Пусть точка $D$ – это точка пересечения продолжения биссектрисы $AA_1$ с описанной окружностью.

По первому свойству $D$ – это центр окружности, описанной около четырехугольника $BOCO_a$.

Следовательно, точка $D$ лежит на серединном перпендикуляре к стороне $BC$, то есть точка $D$ проецируется в точку $M$.

Кроме того, так как $O_aD=DO$, то по теореме Фалеса $PM=MQ$ (так как радиусы проведенные в точку касания перпендикулярны касательной $BC$ и $DM$ - серединный перпендикуляр к $BC$, то $O_aP\parallel DM\parallel OQ$).

Прямая, проведенная через вершину треугольника и точку, в которой вневписанная окружность касается противоположной стороны, делит периметр треугольника пополам. Длина отрезка касательной, проведённой к вневписанной окружности из противоположной вершины, равна полупериметру треугольника.

Рассмотрим треугольник $ABC$.

Пусть вневписанная окружность $\omega_a$ касается прямых $AB, BC$ и $AC$ в точках $N, M$ и $P$ соответственно.

Докажем, что $AB+BM=AC+MC$.

Действительно, так как касательные, проведенные к окружности из одной точки равны, то $AN=AP, BN=BM$ и $CM=CP$.

Учитывая эти соотношения, получаем $AB+BM=AB+BN=AN=AP=AC+CP=AC+CM$.

Таким образом $AN=AB+BN=p$.

$S=r_a(p-a)$.

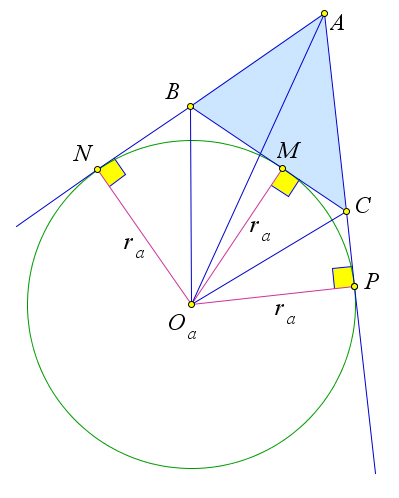
Рассмотрим треугольник $ABC$.

Пусть $\omega_a(O_a,r_a)$ – вневписанная окружность этого треугольника, а $a,b,c$ – его стороны.

Докажем, что $S=r_a(p-a)$.

Пусть $N, M, P$ – это точки касания окружности $\omega_a$ и прямых $AB, BC$ и $AC$ соответственно.

Соединим центр вневписанной окружности $O_a$ с вершинами треугольника.

Тогда

$\displaystyle S_{ABC}=S_{ABO_a}+S_{ACO_a}-S_{BCO_a}=\frac{1}{2}r_ac+\frac{1}{2}r_ab-\frac{1}{2}r_aa=r_a\cdot\frac{b+c-a}{2}=r_a(p-a)$.

$S=\sqrt{rr_ar_br_c}$.

По свойству $4^\circ$ $S=r_a(p-a), S=r_b(p-b), S=r_c(p-c)$.

Кроме того $S=rp$.

Тогда $p=\frac{S}{r}, p-a=\frac{S}{r_a}, p-b=\frac{S}{r_b}, p-c=\frac{S}{r_c}$.

Подставляя эти соотношения в формулу Герона, получим $\displaystyle S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{\frac{S^4}{rr_ar_br_c}}=\frac{S^2}{\sqrt{rr_ar_br_c}}$, или $S=\sqrt{rr_ar_br_c}$.

$S=\dfrac{r_ar_br_c}{p}$.

По свойству $4^\circ$ $S=r_a(p-a), S=r_b(p-b), S=r_c(p-c)$.

Тогда $p=\dfrac{S}{r}, p-a=\dfrac{S}{r_a}, p-b=\dfrac{S}{r_b}, p-c=\dfrac{S}{r_c}$.

Подставляя эти соотношения в формулу Герона, получим $S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{\dfrac{S^3p}{r_ar_br_c}}$.

Возводя это равенство в квадрат и выражая $S$, получим $S=\dfrac{r_ar_br_c}{p}$.

$\displaystyle \frac{1}{r}=\frac{1}{r_a}+\frac{1}{r_b}+\frac{1}{r_c}$.

Напишем цепочку равенств, учитывая свойство $4^\circ$, $\displaystyle\frac{1}{r_a}+\frac{1}{r_b}+\frac{1}{r_c}=\frac{p-a}{S}+\frac{p-b}{S}+\frac{p-c}{S}=\frac{3p-a-b-c}{S}=\frac{3a+3b+3c-2a-2b-2c}{2S}=\frac{a+b+c}{2S}=\frac{p}{S}=\frac{1}{r}$.

$r_ar_b=p(p-c), rr_a=(p-b)(p-c)$.

По свойству $4^\circ$, учитывая формулу Герона, $r_ar_b=\frac{S^2}{(p-a)(p-b)}=\frac{p(p-a)(p-b)(p-c)}{(p-a)(p-b)}=p(p-c)$, $\displaystyle rr_a=\frac{S^2}{p(p-a)}=\frac{p(p-a)(p-b)(p-c)}{p(p-a)}=(p-b)(p-c)$.

Исходный треугольник является ортотреугольником треугольника $O_aO_bO_c$.

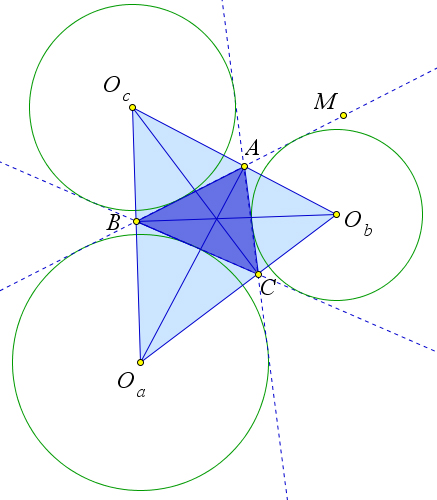
Достаточно доказать, что биссектриса $AO_a$ угла $A$ является высотой треугольника $O_aO_bO_c$, то есть нужно доказать, что $\angle O_aAO_c=90^\circ$.

Отрезки $AO_a$ и $AO_b$ являются биссектрисами смежных углов $\angle BAC$ и $\angle CAM$, следовательно, $\angle O_aAO_c=90^\circ$.

Аналогично $BO_b$ и $CO_c$ являются высотами треугольника $O_aO_bO_c$.

$4R=r_a+r_b+r_c-r$.

Выразим все радиусы через площадь и стороны: $r=\dfrac{S}{p}, R=\dfrac{abc}{4S}, r_a=\dfrac{S}{p-a}, r_b=\dfrac{S}{p-b}, r_c=\dfrac{S}{p-c}$.

Тогда $r_a+r_b+r_c-r=\dfrac{S}{p-a}+\dfrac{S}{p-b}+\dfrac{S}{p-c}-\dfrac{S}{p}=$

$=S\cdot\dfrac{p(p-b)(p-c)+p(p-a)(p-c)+p(p-a)(p-b)-(p-a)(p-b)(p-c)}{p(p-a)(p-b)(p-c)}=$

$=S\dfrac{abc}{S^2}=\dfrac{abc}{S}=4R$

$r_ar_b+r_br_c+r_cr_a=p^2$

Подставим формулы $r=\dfrac{S}{p}, r_a=\dfrac{S}{p-a}, r_a=\dfrac{S}{p-b}, r_a=\dfrac{S}{p-c}$ в левую часть равенства:

$r_ar_b+r_br_c+r_cr_a=\dfrac{S^2}{(p-a)(p-b)}+\dfrac{S^2}{(p-b)(p-c)}+\dfrac{S^2}{(p-c)(p-a)}=$

$=S^2\cdot\dfrac{(p-c)+(p-a)+(p-b)}{(p-a)(p-b)(p-c)}=S^2\cdot\dfrac{p}{(p-a)(p-b)(p-c)}$

Из формулы Герона следует, что $(p-a)(p-b)(p-c)=\dfrac{S^2}{p}$, поэтому

$r_ar_b+r_br_c+r_cr_a=S^2\cdot\dfrac{p^2}{S^2}=p^2$