1. Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле $r=\dfrac{a+b-c}{2}$.
2. Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы, а её центр совпадает с серединой гипотенузы.

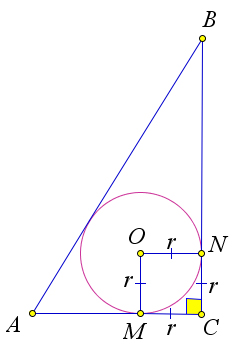
Рассмотрим треугольник $ABC$ с прямым углом $C$.

Пусть в него вписана окружность с центром $O$ и радиусом $r$, которая касается катетов $AC$ и $BC$ в точках $M$ и $N$ соответственно.

Тогда $MONC$ – квадрат, так как все его углы прямые и $MO=ON=r$.

Тогда $CM=r$.

Но $CM=p-c=\dfrac{a+b+c}{2}-c$, то есть $r=\dfrac{a+b-c}{2}$.

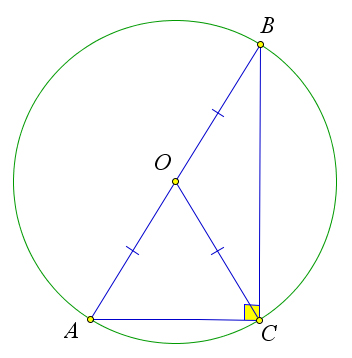
Рассмотрим треугольник $ABC$ с прямым углом $C$.

Пусть $O$ – середина гипотенузы $AB$.

Тогда $OA=OB=OC$, то есть точка $O$ равноудалено от всех вершин треугольника.

Следовательно, точка $O$ является центром окружности, описанной около треугольника $ABC$, радиус которой равен $OA$, то есть половине гипотенузы.