В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.

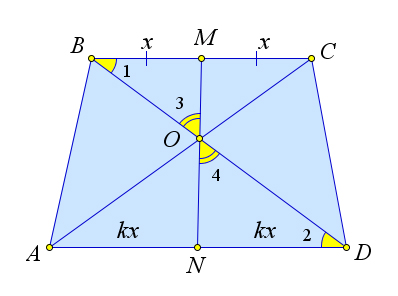
Рассмотрим трапецию $ABCD$.

Пусть продолжения сторон $AB$ и $CD$ пересекаются в точке $P$, точка $M$ – середина основания $BC$, а $N$ – это точка пересечения прямых $PM$ и $AD$.

Докажем, что $N$ – это середина $AD$.

Так как $BC\parallel AD$, то $\triangle BPM\sim \triangle PAN$ и $\triangle PCM\sim\triangle PND$, причем коэффициент подобия в обоих случаях равен $k=\dfrac{PN}{PM}$.

Тогда $AN=k\cdot BM=k\cdot MC=ND$.

Таким образом $N$ – середина $AD$.

Пусть $O$ – точка пересечения диагоналей $AC$ и $BD$.

Докажем, что точка $O$ принадлежит отрезку $MN$.

Треугольники $BOC$ и $AOD$ подобны с коэффициентом $\dfrac{BC}{AD}=\dfrac{BM}{AN}=\dfrac{PM}{PN}=k$.

Следовательно, $\dfrac{BO}{OD}=k$, $\dfrac{BM}{ND}=k$ и $\angle 1=\angle 2$, как накрест лежащие.

Тогда $\triangle BMO\sim\triangle OND$ по второму признаку подобия треугольников.

Следовательно, $\angle 3=\angle 4$, а тогда $MON$ – одна прямая.