Содержание
Гипербола
Определение
Гипербола – это геометрическое место точек, модуль разности расстояний от которых до двух данных точек $F_1$ и $F_2$ постоянен и при этом меньше, чем $|F_1F_2|$.
Теорема
Каноническое уравнение гиперболы имеет вид $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, число $a$ называется вещественной полуосью гиперболы, $b$ – мнимой полуосью.
Доказательство
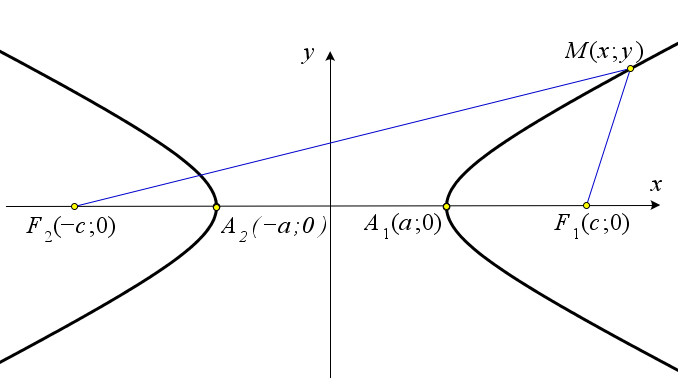
Пусть $M(x,y)$ – это произвольная точка, принадлежащая данной гиперболе, а точки $F_1(c;0)$ и $F_2(-c;0)$ – это её фокусы (рис. \ref{pic159}).
Тогда по определению гиперболы $|MF_1-MF_2|$ постоянен.
Пусть этот модуль равен $2a$, то есть $|MF_1-MF_2|=2a$.
Распишем это равенство с помощью формулы расстояния между двумя точками:
$$|\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}|=2a$$
Возведём это равенство в квадрат, раскроем скобки и приведём подобные слагаемые:
$$2x^2+2c^2+2y^2-2\sqrt{(x-c)^2+y^2}\sqrt{(x+c)^2+y^2}=4a^2$$
или
$$\sqrt{(x-c)^2+y^2}\sqrt{(x+c)^2+y^2}=x^2+y^2+c^2-2a^2.$$
При условии, что $x^2+y^2+c^2-2a^2\geqslant0$, данное уравнение можно возвести в квадрат:
$$((x-c)^2+y^2)((x+c)^2+y^2)=4a^4-4a^2(x^2+y^2+c^2)+(x^2+y^2+c^2)^2$$
или
$$(x^2+c^2+y^2-2xc)(x^2+c^2+y^2+2xc)=4a^4-4a^2x^2-4a^2y^2-4a^2c^2+(x^2+y^2+c^2)^2.$$
В левой части раскроем скобки, используя формулу разности квадратов:
$$(x^2+y^2+c^2)^2-4x^2c^2=4a^4-2a^2x^2-2a^2y^2-2a^2c^2+(x^2+y^2+c^2)^2.$$
Сократив подобные слагаемые, перенеся все слагаемые в одну часть, и сократив на $4$, получим:
$$a^4-a^2x^2-a^2y^2-a^2c^2+x^2c^2=0.$$
Перегруппируем слагаемые:
$$(a^4-a^2c^2)+(x^2c^2-x^2a^2)-a^2y^2=0,$$
$$x^2(a^2-c^2)+a^2y^2=a^2(a^2-c^2).$$
Так как $a<c$, то можно разделить последнее равенство на $a^2(a^2-c^2)$:
$$\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1.$$
Обозначив $b^2=c^2-a^2$, получим
\begin{equation}\label{eq011} \frac{x^2}{a^2}-\frac{y^2}{b^2}=1. \end{equation}
Теперь докажем, что любая пара чисел $(x,y)$, удовлетворяющая последнему равенству, удовлетворяет условию $(x^2+y^2+c^2)-2a^2\geqslant0$.
Преобразуем левую часть:
$$x^2+y^2+c^2-2a^2=x^2+y^2-a^2+(c^2-a^2)=x^2+y^2-a^2+b^2.$$
Из равенства \ref{eq011} следует, что $x^2=a^2\left(1+\frac{y^2}{b^2}\right)\geqslant a^2$, так как $1+\frac{y^2}{b^2}\geqslant 1$.
Следовательно, $x^2\geqslant a^2$, а значит,
$$x^2+y^2-a^2+b^2\geqslant y^2+b^2\geqslant0$$
или
$$x^2+y^2-a^2+b^2\geqslant 0.$$
Следовательно,
$$x^2+y^2+c^2-2a^2\geqslant0.$$
Свойства канонической гиперболы
- Вершины гиперболы имеют координаты $A_{1,2}(\pm a;0)$.
- Каноническая гипербола имеет две асимптоты с уравнениями $y=\pm\frac{b}{a}x$.
- Фокусы канонической гиперболы имеют координаты $F_1(c;0)$ и $F_2(-c;0)$, при этом $b^2=c^2-a^2$ и $c>a$.
- Эксцентриситетом гиперболы называется число $e=\frac{c}{a}$.
Теорема о касательной к гиперболе
Пусть точка $M(x_0;y_0)$ – произвольная точка гиперболы $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$. Тогда уравнение касательной к гиперболе, проведенной в этой точке имеет вид $\frac{xx_0}{a^2}-\frac{yy_0}{b^2}=1$.
Доказательство
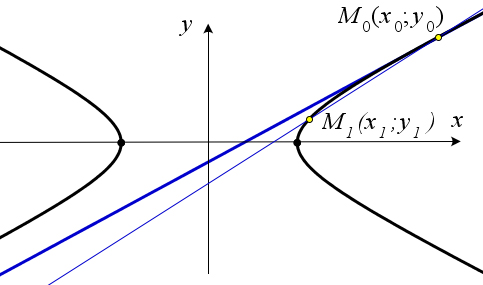
По определению касательной к кривой в данной токе $M$ называется предельное положение секущей $M_0M_1$ при условии, что точка $M_1$ стремится к точке $M_0$ по данной кривой.
Рассмотрим уравнение секущей к эллипсу, проходящей через точку $M_0(x_0;y_0)$ и не совпадающую с ней точку $M_1(x_1;y_1)$.
Поскольку точка $M_1$ стремится к точке $M_0$, знаки их абсцисс совпадают.
Рассмотрим случай, когда абсциссы точек $M_0$ и $M_1$ положительны.
Так как обе точки лежат на гиперболе $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, то их координаты можно записать в виде $M_0(\frac{a}{b}\sqrt{b^2+y_0^2};y_0), M_1(\frac{a}{b}\sqrt{b^2+y_1^2};y_1)$.
Запишем уравнение прямой $M_0M_1$:
$$\frac{x-x_0}{x_0-x_1}=\frac{y-y_0}{y_0-y_1},$$
$$\frac{x-\frac{a}{b}\sqrt{b^2+y_0^2}}{\frac{a}{b}\sqrt{b^2+y_0^2}-\frac{a}{b}\sqrt{b^2+y_1^2}}=\frac{y-y_0}{y_0-y_1},$$
$$\frac{(\frac{b}{a}x-\sqrt{b^2+y_0^2})(\sqrt{b^2+y_0^2}+\sqrt{b^2+y_1^2})}{y_0^2-y_1^2}=\frac{y-y_0}{y_0-y_1},$$
$$(\frac{b}{a}x-\sqrt{b^2+y_0^2})(\sqrt{b^2-y_0^2}+\sqrt{b^2-y_1^2})=(y-y_0)(y_0+y_1).$$
Если точка $M_1$ стремиться к точке $M_0$ по гиперболе, то $y_1$ стремиться к $y_0$.
Тогда последнее равенство можно записать в виде
$$(\frac{b}{a}x-\sqrt{b^2+y_0^2})\cdot2\sqrt{b^2+y_0^2}=(y-y_0)\cdot2y_0,$$
$$\frac{b}{a}x\sqrt{b^2+y_0^2}-b^2-y_0^2=yy_0-y_0^2,$$
$$\frac{b}{a}x\sqrt{b^2+y_0^2}-yy_0=b^2.$$
Разделим это равенство на $b^2$:
$$\frac{1}{ab}x\sqrt{b^2+y_0^2}-\frac{yy_0}{b^2}=1.$$
Учитывая, что $x_0=\frac{a}{b}\sqrt{b^2+y_0^2}$, получаем:
$$\frac{x}{a^2}\cdot\frac{a}{b}\sqrt{b^2+y_0^2}-\frac{yy_0}{b^2}=1,$$
$$\frac{xx_0}{a^2}-\frac{yy_0}{b^2}=1.$$
Случай, когда абсциссы точек $M_0$ и $M_1$ отрицательны рассматривается аналогично, с той лишь разницей, что теперь координаты этих точек будут иметь вид $M_0(-\frac{a}{b}\sqrt{b^2+y_0^2};y_0), M_1(-\frac{a}{b}\sqrt{b^2+y_1^2};y_1)$.
Лемма
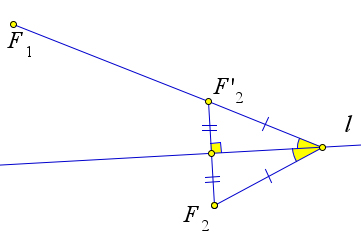
Максимум модуля разности расстояний от точки данной прямой $l$ до точек $F_1$ и $F_2$, лежащих по разные стороны от данной прямой достигается в такой точке $P$, для которой лучи $PF_1$ и $PF_2$ образуют равные углы с прямой $l$.
Доказательство
Обозначим через $F_2'$ точку, симметричную $F_2$ относительно прямой $l$.
Очевидно, что $F_2X=F_2'X$ для любой точки $X$ на прямой $l$.
Нам достаточно найти такую точку $P$, что разность расстояний от $P$ до $F_1$ и $F_2'$ будет как можно больше.
Из неравенства треугольника следует, что $|F_1P-F_2'P|<F_1F_2'$.
И достигается этот максимум тогда и только тогда, когда точки $F_1, F_2, P$ лежат на одной прямой.
Поскольку точки $F_2$ и $F_2'$ симметричны, углы, которые образуют прямые $F_1P$ и $F_2P$ с прямой $l$, равны.
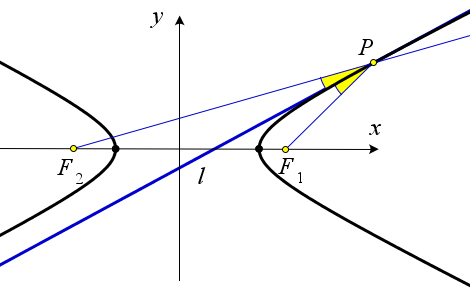
Оптическое свойство гиперболы
Луч света, вышедший из фокуса $F_2$, отразившись от какой-либо точки $M$ гиперболы, распространяется далее вдоль луча $F_1M$, то есть так, как если бы луч света исходил из фокуса $F_1$ и распространялся бы без помех.
Доказательство
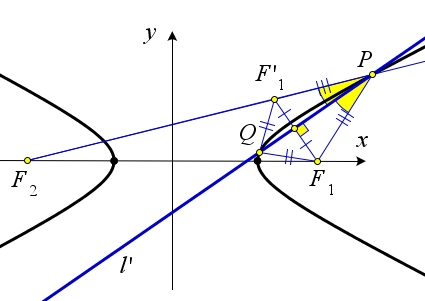
Переформулируем утверждение: если прямая $l$ касается гиперболы в точке $P$, то $l$ является биссектрисой угла $F_1PF_2$, где $F_1$ и $F_2$ – фокусы гиперболы.
Предположим, что биссектриса $l'$ угла $F_1PF_2$ пересекает гиперболу ещё в какой-нибудь точке $Q$ (лежащей на той же дуге, что и $P$).
Для удобства будем считать, что точка $P$ лежит на дуге, которая ближе к фокусу $F_1$.
Обозначим через $F_1'$ точку, симметричную $F_1$ относительно $l'$. Тогда $F_1Q=QF_1'$, $F_1P=PF_1'$;
кроме того, точки $F_2, F_1'$ и $P$ лежат на одной прямой.
Итак, $F_2P-PF_1=F_2Q-F_1Q$. В силу вышеуказанных равенств получаем $F_2F_1'=F_2P-PF_1'=F_2Q-QF_1'$.
Но по неравенству треугольника $F_2F_1'>F_2Q-QF_1'$.
Таким образом получено противоречие, что и доказывает утверждение теоремы.