Содержание
Отношение площадей треугольников с равными элементами
Теорема
- Если высоты двух треугольников равны, то их площади относятся, как основания.
- Если основания двух треугольников равны, то их площади относятся, как высоты, проведенные к этим основаниям.
- Если угол одного треугольника равен углу другого треугольника, то их площади относятся, как произведения сторон, заключающих равные углы.
Докажем первый пункт теоремы.
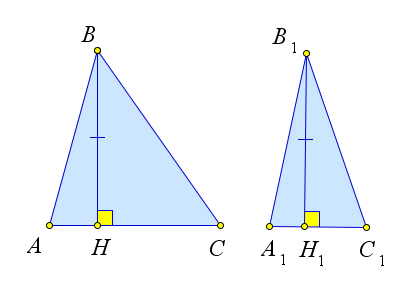
Рассмотрим треугольники $\triangle ABC$ и $\triangle A_1B_1C_1$ в которых высоты $BH$ и $B_1H_1$ равны.
Тогда $\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{\frac{1}{2}BH\cdot AC}{\dfrac{1}{2}B_1H_1\cdot A_1C_1}=\dfrac{AC}{A_1C_1}$.
Докажем второй пункт теоремы.
Рассмотрим треугольники $\triangle ABC$ и $\triangle A_1B_1C_1$ в которых основания $AC$ и $A_1C_1$ равны.
Тогда $\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{\dfrac{1}{2}BH\cdot AC}{\dfrac{1}{2}B_1H_1\cdot A_1C_1}=\dfrac{BH}{B_1H_1}$.
Докажем третий пункт теоремы.
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$ в которых углы $A$ и $A_1$ равны.
Докажем, что их площади относятся как произведения сторон, заключающих эти углы.
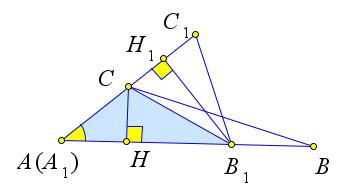
Наложим треугольник $A_1B_1C_1$ на треугольник $ABC$ так, чтобы вершина $A_1$ совместилась с вершиной $A$, а стороны $A_1B_1$ и $A_1C_1$ наложились соответственно на лучи $AB$ и $AC$.
Треугольники $ABC$ и $AB_1C$ имеют общую высоту $CH$, поэтому $\dfrac{S_{ABC}}{S_{AB_1C}}=\dfrac{AB}{AB_1}$.
Треугольники $AB_1C$ и $AB_1C_1$ имеют общую высоту $B_1H_1$, поэтому $\dfrac{S_{AB_1C}}{S_{AB_1C_1}}=\dfrac{AC}{AC_1}$.
Перемножая полученные равенства, находим: $\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}$.
Свойство биссектрисы треугольника
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим его сторонам.
Доказательство
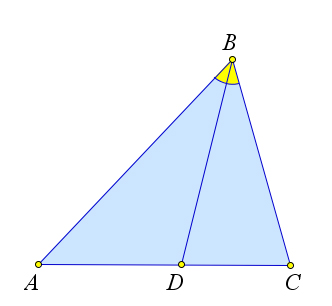
Рассмотрим треугольник $ABC$, в котором проведена биссектриса $BD$.
Докажем, что $\dfrac{AD}{DC}=\dfrac{AB}{BC}$.
Действительно, так как у треугольников $ABD$ и $BDC$ высота, проведенная из вершины $B$, общая, то $S_{ABD}:S_{BDC}=AD:DC$.
Кроме того у этих треугольников есть равные углы, следовательно их площади относятся, как произведения сторон: $S_{ABD}:S_{BDC}=\dfrac{AB\cdot BD}{BD\cdot BC}=\dfrac{AB}{BC}$.
Сравнивая полученные равенства для отношения площадей, получаем: $\dfrac{AD}{DC}=\dfrac{AB}{BC}$.
Теорема об инцентре
- Инцентр делит биссектрису $l_c$ в отношении $(a+b):c$
- Все биссектрисы треугольника пересекаются в одной точке.
Доказательство
Докажем первый пункт теоремы
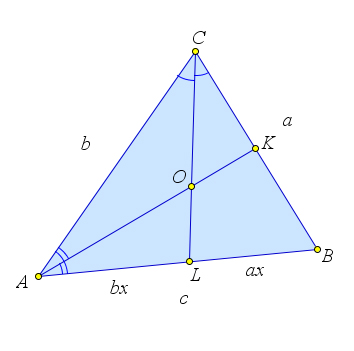
Рассмотрим треугольник $ABC$, в котором проведены биссектрисы $AK$ и $CL$.
Пусть $BC=a, AC=b, AB=c$.
Пусть $AK$ пересекает $CL$ в точке $O$.
По теореме $AL:LB=b:a$.
Тогда $AL=c\cdot\dfrac{b}{a+b}$
Кроме того в треугольнике $ACL$, $AO$ – биссектриса.
Тогда $CO:OL=b:AL=b:\left(\dfrac{bc}{a+b}\right)=\dfrac{a+b}{c}$.
Докажем второй пункт теоремы
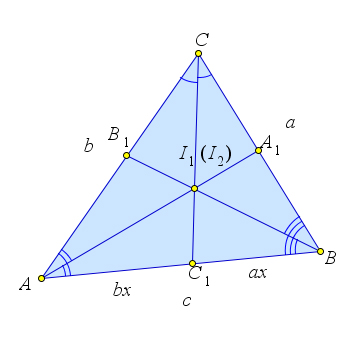
Рассмотрим треугольник $ABC$, в котором проведены биссектрисы $AA_1$, $BB_1$ и $CC_1$.
Пусть $BC=a, AC=b, AB=c$.
Пусть $AA_1\cap CC_1=I_1$, $BB_1\cap CC_1=I_2$.
Тогда по теореме $CI_1:I_1C_1=\dfrac{a+b}{c}$ и $CI_2:I_2C_1=\dfrac{a+b}{c}$.
А это означает, что точки $I_1$ и $I_2$ совпадают (так как они обе лежат на отрезке $CC_1$).
Таким образом все биссектрисы пересекаются в одной точке.
Доптеоремы
О шести треугольниках и медианах
О боковых треугольниках трапеции
О произведении площадей в четырехугольнике с диагоналями и следствие для трапеции