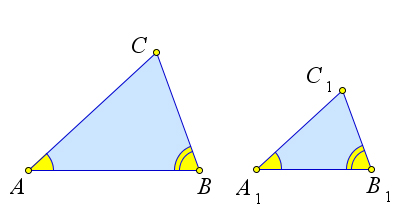
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Доказательство
Первый способ (без использования тригонометрии).
Пусть $\triangle ABC$ и $\triangle A_1B_1C_1$ – два треугольника, у которых $\angle A=\angle A_1,
\angle B=\angle B_1$.
Докажем, что $\triangle ABC\sim\triangle A_1B_1C_1$.
По теореме о сумме углов треугольника $\angle C=180^\circ-\angle A-\angle B=180^\circ-\angle A_1-\angle B_1=\angle C_1$.
Докажем, что стороны треугольника $ABC$ пропорциональны
сходственным сторонам треугольника $A_1B_1C_1$.
Так как $\angle A=\angle A_1$ и $\angle C=\angle C_1$, то
$\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{AB\cdot AC}{A_1B_1\cdot
A_1C_1}$ и $\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{CA\cdot
CB}{C_1A_1\cdot C_1B_1}$.
Из этих равенств следует, что
$\dfrac{AB}{A_1B_1}=\dfrac{BC}{B_1C_1}$.
Аналогично, используя
равенство $\angle A=\angle A_1$, $\angle B=\angle B_1$, получаем, что
$\dfrac{BC}{B_1C_1}=\dfrac{CA}{C_1A_1}$.
Итак, стороны треугольника $ABC$ пропорциональны сторонам треугольника $A_1B_1C_1$.
Второй способ (через тригонометрию).
Пусть $\triangle ABC$ и $\triangle A_1B_1C_1$ – два треугольника, у которых $\angle A=\angle A_1, \angle B=\angle B_1$.
Докажем, что $\triangle ABC\sim\triangle A_1B_1C_1$.
По теореме о сумме углов треугольника $\angle C=180^\circ-\angle A-\angle
B=180^\circ-\angle A_1-\angle B_1=\angle C_1$.
Докажем, что стороны треугольника $ABC$ пропорциональны
сходственным сторонам треугольника $A_1B_1C_1$.
Так как $\angle A=\angle A_1$ и $\angle B=\angle B_1$, то по теореме синусов:
$\dfrac{a}{b}=\dfrac{\sin{A}}{\sin{B}}=\dfrac{\sin{A_1}}{\sin{B_1}}=\dfrac{a_1}{b_1}$,
следовательно $\dfrac{a}{a_1}=\dfrac{b}{b_1}$.
Аналогично можно
получить, что $\dfrac{a}{a_1}=\dfrac{c}{c_1}$.
Следовательно, $\dfrac{a}{a_1}=\dfrac{b}{b_1}=\dfrac{c}{c_1}$.