Содержание
Свойства параллелограмма
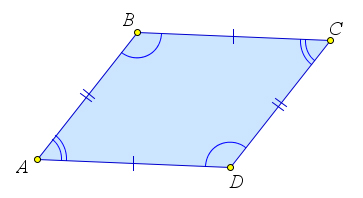
- В параллелограмме противоположные стороны равны и противоположные углы равны.
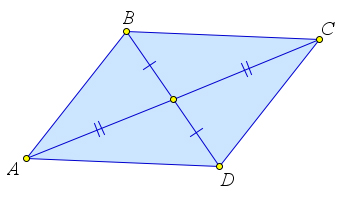
- Диагонали параллелограмма точкой пересечения делятся пополам.
Доказательство.
Докажем первый пункт теоремы.
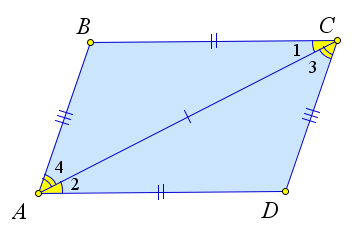
Проведем в параллелограмме $ABCD$ диагональ $AC$.
По определению параллелограмма $AB\parallel CD$ и $BC\parallel AD$.
Следовательно, $\angle 1=\angle 2, \angle
3=\angle 4$.
Тогда треугольники $ABC$ и $ADC$ равны по второму признаку
равенства ($AC$ – общая).
Следовательно, $AB=CD, BC=AD$.
Докажем второй пункт теоремы.
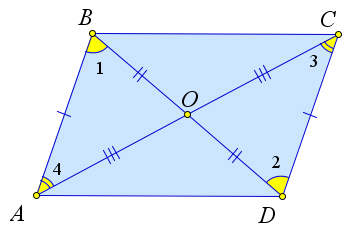
Пусть диагонали $AC$ и $BD$ параллелограмма $ABCD$ пересекаются в точке
$O$.
По определению параллелограмма $AB\parallel CD$, следовательно, $\angle 1=\angle 2, \angle 3=\angle 4$, как накрест лежащие.
Кроме того $AB=CD$ по первому пункту теоремы, следовательно, $\triangle
ABO=\triangle CDO$.
Из равенства этих треугольников следует, что $AO=OC$ и $BO=OD$.
Замечание
Полезно иметь ввиду, что
- Сумма углов параллелограмма, прилежащих к одной стороне, равна $180^\circ$.
- Диагональ параллелограмма делит его на два равных треугольника.
- Диагонали параллелограмма делят его на две пары равных треугольников.