Содержание
Трапеция
Определение
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Замечание
Сумма углов при боковой стороне трапеции равна $180^\circ$.
Доказательство
Действительно, так как основания трапеции параллельны, а боковая сторона является секущей, то углы при боковой стороне являются внутренними односторонними углами при параллельных прямых, и, следовательно, их сумма равна $180^\circ$.
Определение
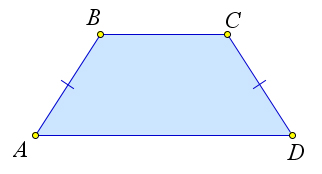
- Трапеция называется равнобедренной, если ее боковые стороны равны.
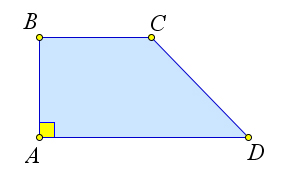
- Трапеция называется прямоугольной, если один из ее углов равен $90^\circ$.
Свойства равнобедренной трапеции
- Углы при основании равнобедренной трапеции равны.
- Диагонали равнобедренной трапеции равны.
- Диагонали равнобедренной трапеции, пересекаясь, образуют два равных и два равнобедренных треугольника.
- Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Доказательство
Докажем первый пункт теоремы.
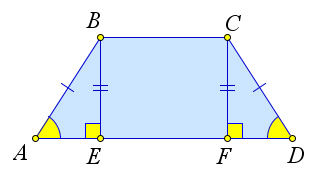
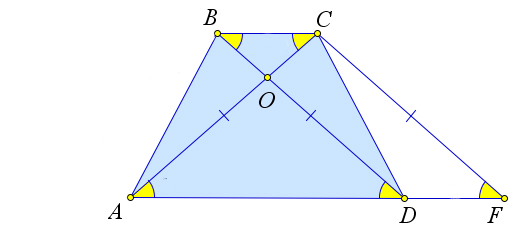
Рассмотрим равнобедренную трапецию $ABCD$, $AB=CD$.
Докажем, что $\angle A=\angle D$.
Проведем из точек $B$ и $C$ высоты $BE$ и $CF$.
Треугольники $\triangle ABE$ и $\triangle CFD$ равны по катету и гипотенузе ($AB=CD, BE=CF$).
Следовательно, $\angle A=\angle D$.
Докажем второй пункт теоремы.
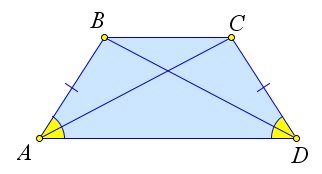
В равнобедренной трапеции $ABCD$ рассмотрим треугольники $\triangle ABD$ и $\triangle ACD$.
Они равны по первому признаку ($AB=CD$, $AD$ – общая, $\angle A=\angle D$ по первому пункту).
Следовательно, $AC=BD$.
Докажем третий пункт теоремы.
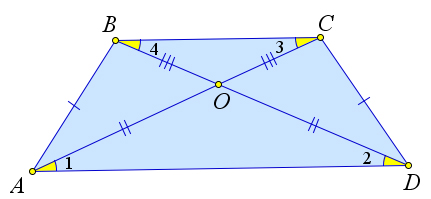
Пусть диагонали равнобедренной трапеции $ABCD$ пересекаются в точке $O$. Докажем, что треугольники $\triangle AOD$ и $\triangle BOC$ – равнобедренные, а треугольники $\triangle AOB$ и $\triangle COD$ равны.
Действительно, во втором пункте уже было доказано, что $\triangle ABD=\triangle ACD$.
Следовательно, $\angle 1=\angle 2$, а так как они накрест лежащие с углами $\angle 3$ и $\angle 4$ соответственно, то $\angle 3=\angle 4$, что и означает, что треугольники $\triangle AOD$ и $\triangle BOC$ – равнобедренные.
Тогда $AO=OD$ и $BO=OC$, и как следствие, $\triangle AOB=\triangle COD$ по третьему признаку равенства треугольников.
Докажем четвертый пункт теоремы.
Так как $\triangle AEB=\triangle CFD$ (по катету и гипотенузе), то $AE=FD$.
Кроме того, $EF=BC$, следовательно, $AE=\dfrac{AD-BC}{2}$ и $AF=\dfrac{AD-BC}{2}+BC=\dfrac{AD+BC}{2}$.
Признаки равнобедренной трапеции
- Если углы при основании трапеции равны, то она равнобедренная.
- Если диагонали трапеции равны, то она равнобедренная.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим трапецию $ABCD$, в которой $\angle A=\angle D$.
Докажем, что тогда $AB=CD$, то есть трапеция равнобедренная.
Проведем из вершины $C$ отрезок $CE$ параллельный стороне $AB$.
Тогда $\angle A=\angle CED$, как соответственные углы.
Следовательно, $\angle CED=\angle D$, а тогда $\triangle CED$ – равнобедренный.
А поскольку $AB=CE$ ($ABCE$ – параллелограмм), то $AB=CD$.
Докажем второй пункт теоремы.
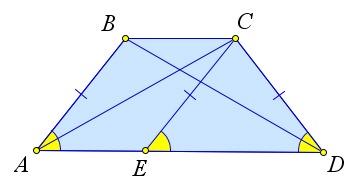
Рассмотрим трапецию $ABCD$, у которой $AC=BD$.
Докажем, что тогда $AB=CD$.
Построим из точки $C$ прямую, параллельный диагонали $BD$. Пусть она пересекает прямую $AD$ в точке $F$.
Тогда $BD=CF$, так как $BCFD$ – параллелограмм по определению.
Тогда $\triangle ACF$ – равнобедренный, так как $AC=CF$.
Следовательно $\angle OAD=\angle ODA$, и $\triangle AOD$ – равнобедренный.
Тогда $AO=OD$ и $BO=OC$.
Следовательно, $\triangle BOA=\triangle COD$ по первому признаку ($\angle BOA=\angle COD$ - как вертикальные).
Следовательно, $AB=CD$.
Теорема (о равнобедренной трапеции с перпендикулярными диагоналями)
Доказательство
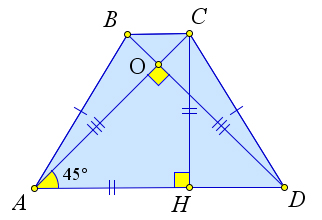
Рассмотрим равнобедренную трапецию $ABCD$, в которой $AC\perp BD$.
Докажем, что в такой трапеции высота $CH$ равна средней линии то есть полусумме оснований.
Действительно, $\triangle AOD$ – равнобедренный и прямоугольный, следовательно, $\angle OAD = 45^\circ$. Тогда $\triangle AHC$ – равнобедренный, то есть $AH=CH$.
Но отрезок $AH$ равен полусумме оснований.