Содержание
Углы в окружности
Определение
Угол с вершиной в центре окружности называется ее центральным углом.
Определение
Градусной мерой дуги окружности называется величина центрального угла, который соответствует этой дуге.
Определение
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Теоерема о вписанном угле
Доказательство
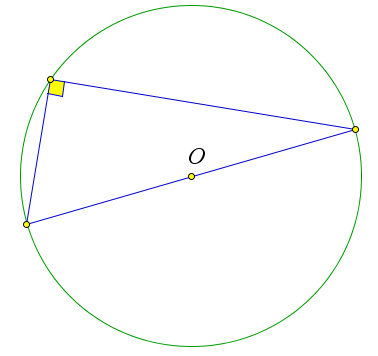
Пусть $\a ABC$ – вписанный угол окружности с центром $O$, опирающийся на дугу $AC$.
Докажем, что $\angle ABC=\frac{1}{2}\buildrel\,\,\frown\over{AC}$.
Рассмотрим три возможных случая расположения луча $BO$ относительно угла $ABC$.
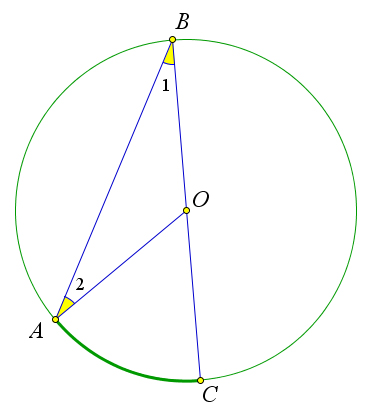
Первый случай.
Пусть луч $BO$ совпадает с одной из сторон угла $ABC$, например со стороной $BC$.
В этом случае дуга $AC$ меньше полуокружности, поэтому $\a AOC=\buildrel\,\,\frown\over{AC}$.
Так как угол $AOC$ – внешний угол равнобедренного треугольника $ABO$, и $\angle 1=\angle 2$, как углы при основании равнобедренного треугольника, то $\angle AOC=\angle 1+\angle 2=2\angle 1$.
Отсюда следует, что $2\angle 1=\buildrel\,\,\frown\over{AC}$ или $\angle ABC=\angle 1=\frac{1}{2}\buildrel\,\,\frown\over{AC}$.
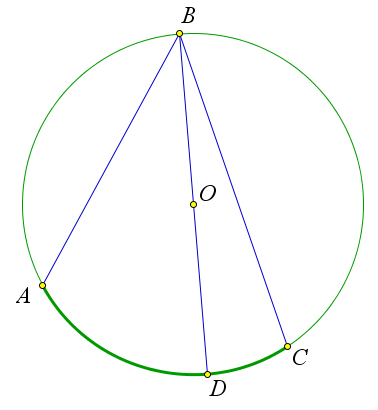
Второй случай.
Пусть луч $BO$ делит угол $ABC$ на два угла.
В этом случае луч $BO$ пересекает дугу $\buildrel\,\,\frown\over{AC}$ в некоторой точке $D$.
Точка $D$ разделяет дугу $\buildrel\,\,\frown\over{AC}$ на две дуги: $\buildrel\,\,\frown\over{AD}$ и $\buildrel\,\,\frown\over{DC}$.
По первому случаю $\angle ABD=\frac{1}{2}\buildrel\,\,\frown\over{AD}$ и $\angle DBC=\frac{1}{2}\buildrel\,\,\frown\over{DC}$.
Складывая эти равенства, получим: $\angle ABD+\angle DBC=\frac{1}{2}\buildrel\,\,\frown\over{AD}+\frac{1}{2}\buildrel\,\,\frown\over{DC}=\frac{1}{2}\buildrel\,\,\frown\over{AC}$.
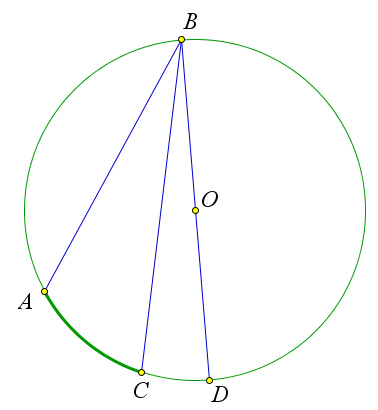
Третий случай.
Пусть луч $BO$ пересекает окружность в точке $D$, при этом луч $BC$ разбивает угол $ABD$ на два угла.
Точка $C$ разделяет дугу $\buildrel\,\,\frown\over{AD}$ на две дуги: $\buildrel\,\,\frown\over{AC}$ и $\buildrel\,\,\frown\over{CD}$.
По первому случаю $\angle ABD=\frac{1}{2}\buildrel\,\,\frown\over{AD}$ и $\angle DBC=\frac{1}{2}\buildrel\,\,\frown\over{DC}$.
Вычитая эти равенства, получим: $\angle ABD-\angle CBD=\frac{1}{2}\buildrel\,\,\frown\over{AD}-\frac{1}{2}\buildrel\,\,\frown\over{CD}=\frac{1}{2}\buildrel\,\,\frown\over{AC}$.
Следствие
Следствие
Теорема
- Угол между пересекающимися хордами окружности равен полусумме двух противоположных дуг, высекаемых этими хордами.
- Угол между двумя пересекающимися секущими данной окружности равен полуразности дуг, высекаемых этими секущими.
- Угол между двумя пересекающимися касательными к окружности равен $180^\circ-\alpha$, где $\alpha$ – градусная мера меньшей из дуг, образованных точками касания.
- Угол между касательной и хордой, проведенной из точки касания, равен половине дуги, заключенной между ними.
- Угол между касательной и секущей, равен полуразности дуг, которые они высекают.
Доказательство
Докажем первый пункт теоремы.
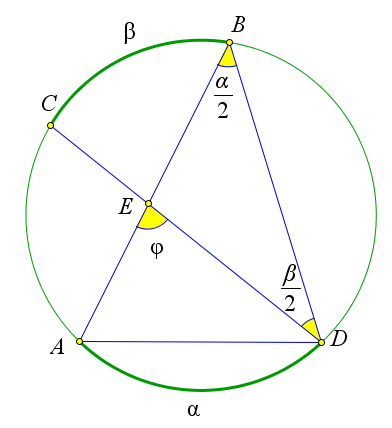
Пусть хорды $AB$ и $CD$ окружности $\omega$ пересекаются в точке $E$.
Обозначим $\angle \varphi=\angle AED, \alpha=\buildrel\,\,\frown\over{AD}, \beta=\buildrel\,\,\frown\over{BC}$.
Докажем, что $\angle \varphi=\frac{\alpha+\beta}{2}$.
Углы $ABD$ и $CDB$ – вписанные, поэтому $\angle ABD=\frac{\alpha}{2}, \angle CDB=\frac{\beta}{2}$.
Кроме того $\angle \varphi$ – внешний угол треугольника $EBD$, поэтому $\angle \varphi=\frac{\alpha}{2}+\frac{\beta}{2}=\frac{\alpha+\beta}{2}$.
Докажем второй пункт теоремы.
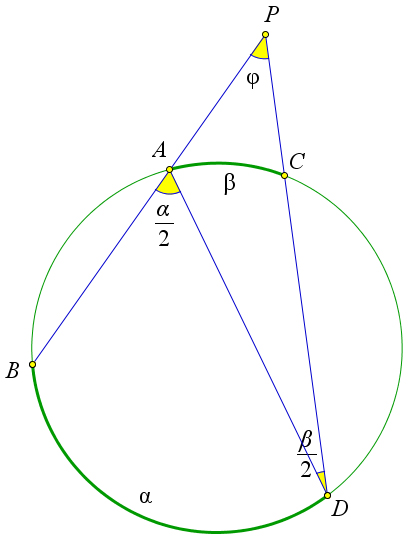
Пусть секущие $PB$ и $PD$ пересекают окружность $\omega$ в точках $A$ и $C$ соответственно.
Обозначим $\alpha = \buildrel\,\,\frown\over{BD}, \beta=\buildrel\,\,\frown\over{AC}, \angle \varphi=\angle P$.
Докажем, что тогда $\varphi=\frac{\alpha-\beta}{2}$.
Углы $BAD$ и $ADC$ – вписанные, поэтому $\angle BAD=\frac{\alpha}{2}, \angle ADC=\frac{\beta}{2}$.
Кроме того $\angle BAD$ – внешний угол треугольника $PAD$, следовательно, $\frac{\alpha}{2}=\angle \varphi+\frac{\beta}{2}$, откуда $\angle \varphi=\frac{\alpha-\beta}{2}$.
Докажем третий пункт теоремы.
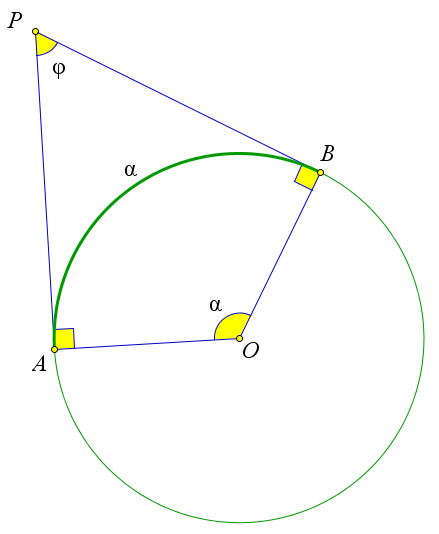
Пусть из точки $P$ к окружности с центром $O$ проведены две касательные $PA$ и $PB$ ($A$ и $B$ – точки касания).
Обозначим $\buildrel\,\,\frown\over{AB}=\alpha$.
Угол $AOB$ – центральный, поэтому $\angle AOB=\alpha$.
Кроме того $\angle PAO=\angle PBO=90^\circ$.
Поскольку сумма углов четырехугольника $PAOB$ равна $360^\circ$, то $\angle P=\angle \varphi=360^\circ-90^\circ-90^\circ-\alpha=180^\circ-\alpha$.
Докажем четвертый пункт теоремы.
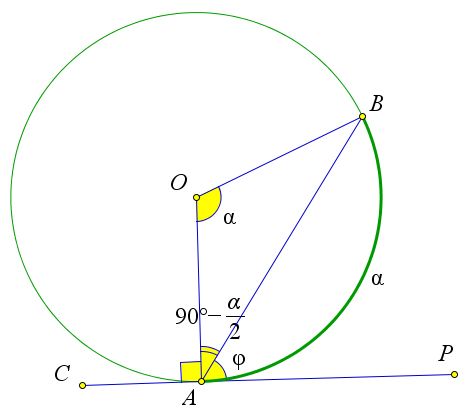
Пусть прямая $PC$ касается окружности с центром $O$ в точке $A$.
Кроме того пусть проведена хорда $AB$.
Обозначим $\alpha=\buildrel\,\,\frown\over{AB}$.
Докажем, что тогда $\angle PAB=\frac{\alpha}{2}$.
Угол $AOB$ центральный, поэтому он равен $\alpha$.
Кроме того, треугольник $AOB$ равнобедренный, следовательно, $\angle OAB=\frac{180^\circ-\alpha}{2}=90^\circ-\frac{\alpha}{2}$.
Угол $OAP$ равен $90^\circ$, так как это угол между касательной и радиусом.
Тогда $\angle \varphi=\angle PAB=90^\circ-(90^\circ-\frac{\alpha}{2})=\frac{\alpha}{2}$.
Докажем пятый пункт теоремы.
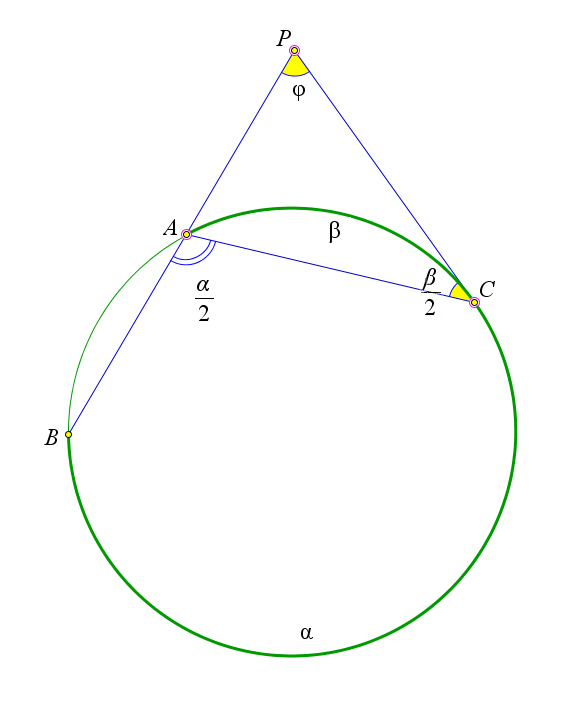
Пусть секущая $PB$ пересекает окружность в точке $A$, $PC$ – касательная.
Обозначим $\alpha=\buildrel\,\,\frown\over{BC}$, $\beta=\buildrel\,\,\frown\over{AC}$, $\varphi=\angle APC$.
Докажем, что тогда $\varphi=\dfrac{\alpha-\beta}{2}$.
Угол $\angle BAC$ равен половине дуги $\buildrel\,\,\frown\over{BC}$, то есть $\angle BAC=\dfrac{\alpha}{2}$.
Угол $\angle ACP$ – это угол между касательной и хордой, следовательно он равен половине дуги $\buildrel\,\,\frown\over{AC}$, то есть $\angle ACP=\dfrac{\beta}{2}$.
Угол $\angle BAC$ – внешний для треугольника $\triangel PAC$, следовательно $\angle BAC=\angle APC+\angle PCA$, или иначе $\dfrac{\alpha}{2}=\varphi+\dfrac{\beta}{2}$.
Откуда $\varphi=\dfrac{\alpha-\beta}{2}$.