Это старая версия документа!
Содержание
$\newcommand{\updownarrows}{\uparrow\!\downarrow}$ $\newcommand{\tg}{\mathop{\rm tg}\nolimits}$ $\newcommand{\ctg}{\mathop{\rm ctg}\nolimits}$ $\newcommand{\sign}{\mathop{\rm sign}\nolimits}$ $\newcommand{\arctg}{\mathop{\rm arctg}\nolimits}$ $\newcommand{\arcctg}{\mathop{\rm arcctg}\nolimits}$ $\newcommand{\deg}{^\circ}$ $\newcommand{\a}{\angle}$ $\newcommand{\archat}{\arc\buildrel\,\,\frown\over}$ $\newcommand{\Vec}{\overrightarrow}$
Ортоцентр
Теорема об ортоцентрической системе точек
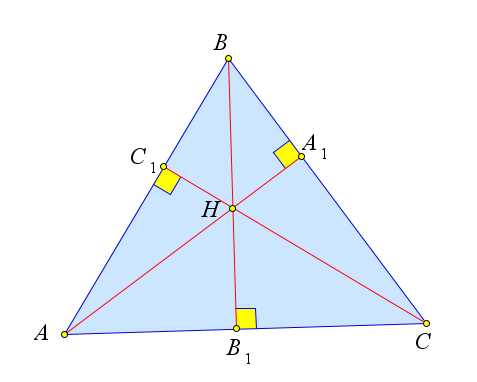
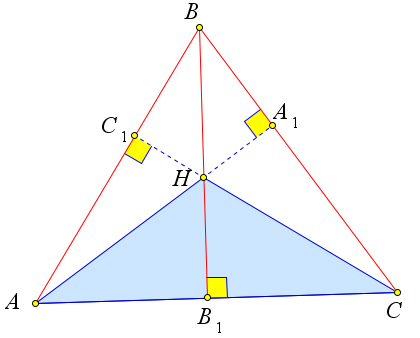
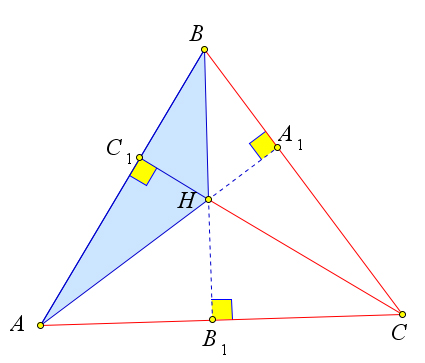
Если в четвёрке точек $A, B, C, H$ точка $H$ является точкой пересечения высот треугольника $ABC$, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками.
Доказательство
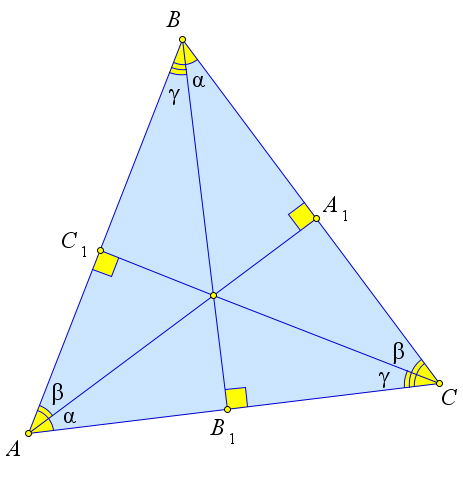
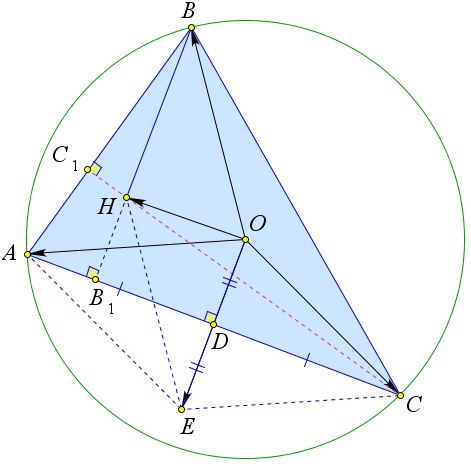
Рассмотрим треугольник $ABC$, в котором $AA_1, BB_1, CC_1$ – это высоты, точка $H$ – это ортоцентр.
Докажем, что точка $A$ – это ортоцентр треугольника $BCH$.
Действительно, для треугольника $BCH$ высотами являются $BC_1, HA_1$ и $B_1C$.
А прямые, содержащие эти отрезки, пересекаются в точке $A$.
Аналогично точки $B$ и $C$ являются ортоцентрами для треугольников $ACH$ и $ABH$ соответственно.
Теорема
Доказательство
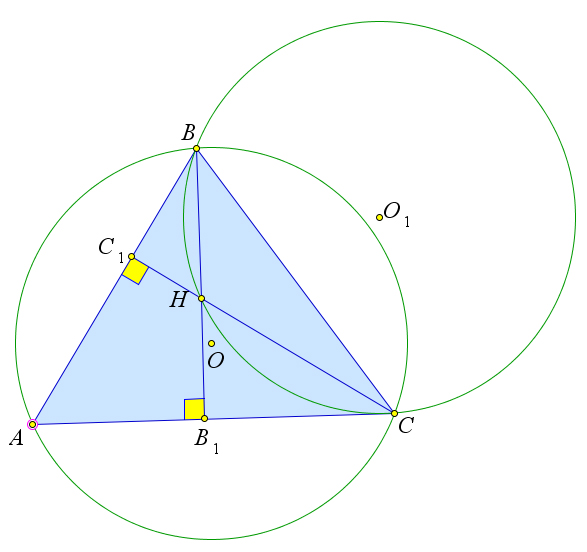
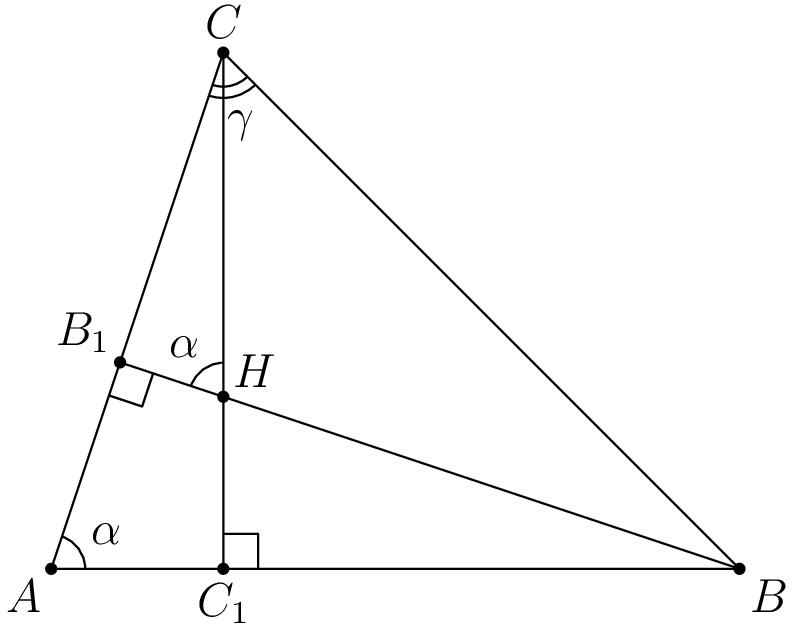
Рассмотрим треугольник $ABC$, в котором высоты $BB_1$ и $CC_1$ пересекаются в точке $H$.
Докажем, что радиусы окружностей $\omega$ и $\omega_1$, описанных соответственно около треугольников $ABC$ и $BCH$, равны.
В четырёхугольнике $AC_1HB_1$ углы $C_1$ и $B_1$ прямые.
А так как сумма углов четырёхугольника равна $360^\circ$, то $\angle CHB=180^\circ-\angle A$, и, следовательно, синусы этих углов равны.
Радиусы рассматриваемых окружностей выражаются по формулам $R=\dfrac{BC}{2\sin{\angle A}}, R_1=\dfrac{BC}{2\sin{\angle CHB}}$.
Но так как синусы $\angle A$ и $\angle CHB$ равны, то и радиусы $R$ и $R_1$ равны.
Теорема
В остроугольном треугольнике $ABC$ с высотами $AA_1, BB_1, CC_1$ выполняются следующие соотношения:
- $\angle A_1AC=\angle B_1BC,$
- $\angle C_1CB=\angle A_1AB,$
- $\angle B_1BA=\angle C_1CA.$
Доказательство
Рассмотрим треугольник $ABC$ с высотами $AA_1, BB_1, CC_1$.
В прямоугольных треугольниках $AA_1C$ и $BB_1C$ острый угол $C$ является общим, поэтому другие острые углы равны: $\angle A_1AC=\angle B_1BC$.
Аналогично в треугольниках $A_1AB$ и $C_1CB$ есть общий острый угол $B$, а в треугольниках $B_1BA$ и $C_1CA$ есть общий острый угол $A$.
Следовательно, другие острые углы в этих парах треугольников равны между собой: $\angle C_1CB=\angle A_1AB, \angle B_1BA=\angle C_1CA.$
Теорема
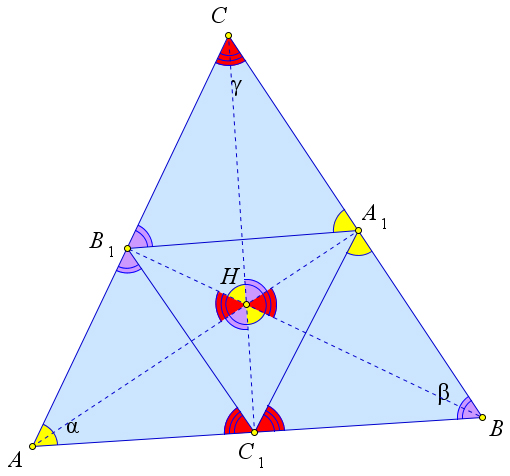
В остроугольном треугольнике $ABC$ с высотами $AA_1, BB_1, CC_1$ и ортоцентром $H$ выполняются следующие соотношения:
- $\angle A=\angle B_1HC=\angle C_1HB=\angle B_1A_1C=\angle C_1A_1B,$
- $\angle B=\angle A_1HC=\angle C_1HA=\angle C_1B_1A=\angle A_1B_1C,$
- $\angle C=\angle B_1HA=\angle A_1HB=\angle B_1C_1A=\angle A_1C_1B.$
Доказательство
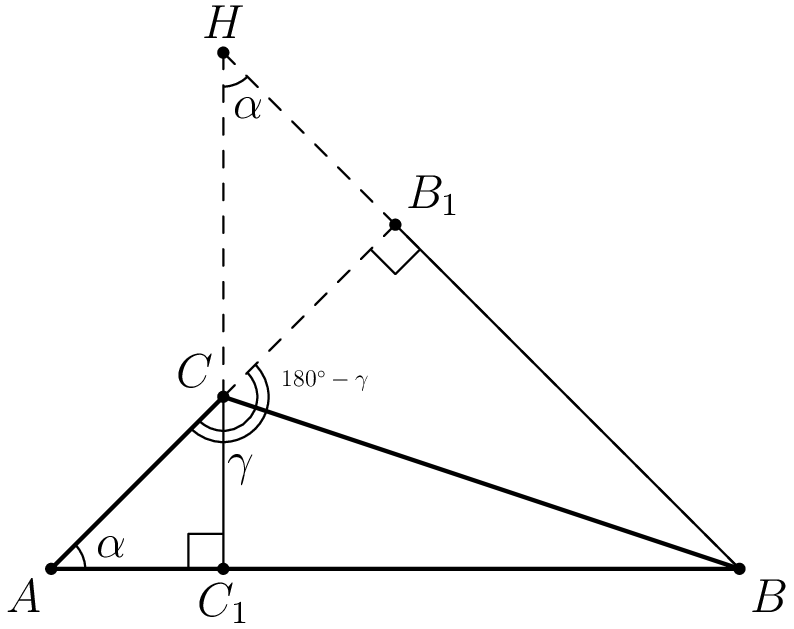
Обозначим $\alpha=\angle A, \beta=\angle B, \gamma=\angle C$.
В прямоугольных треугольниках $ACC_1$ и $CB_1H$ есть общий острый угол $\angle ACC_1$, следовательно, другие острые углы в этих треугольниках равны: $\angle A=\angle B_1HC=\alpha$.
Кроме того $\angle C_1HB=\angle B_1HC=\alpha$, как вертикальные.
Заметим, что $\angle CAA_1=\angle B_1BC$.
Выпишем синусы этих углов из прямоугольных треугольников $CAA_1$ и $BB_1C$: $\sin{\angle CAA_1}=\dfrac{A_1C}{AC}$, $\sin{\angle B_1BC}=\dfrac{B_1C}{BC}$.
Значит, $\dfrac{A_1C}{AC}=\dfrac{B_1C}{BC}$ или $\dfrac{A_1C}{B_1C}=\dfrac{AC}{BC}$.
Тогда $\triangle A_1B_1C\sim\triangle ABC$ по второму признаку подобия (угол $C$ – общий, а стороны $CA_1$ и $CB_1$ пропорциональны сторонам $CA$ и $CB$).
Тогда углы этих треугольников, лежащие напротив пропорциональных сторон, равны: $\angle CA_1B_1=\angle A=\alpha, \angle CB_1A_1=\angle B=\beta$.
Аналогично из подобия треугольников $A_1BC_1$ и $ABC$ получаем $\angle BA_1C_1=\angle A=\alpha, \angle BC_1A_1=\angle C=\gamma$.
Таким образом $\angle A=\angle B_1HC=\angle C_1HB=\angle B_1A_1C=\angle C_1A_1B$.
Аналогично можно получить и остальные соотношения.
Теорема
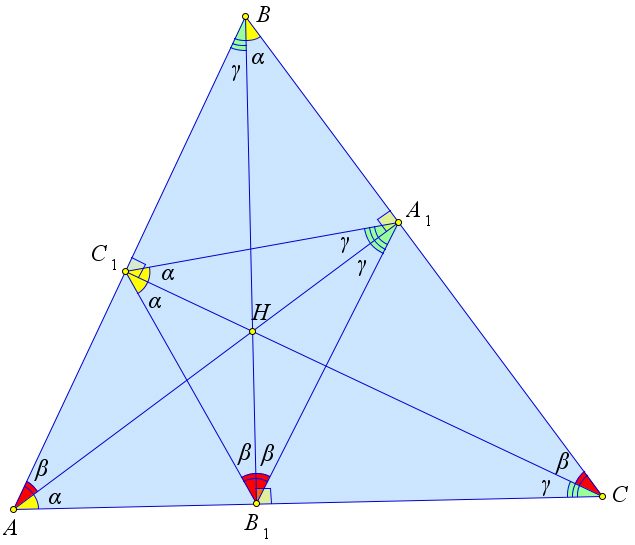
В остроугольном треугольнике $ABC$ с высотами $AA_1, BB_1, CC_1$ и ортоцентром $H$ выполняются следующие соотношения:
- $\angle B_1BC=\angle CC_1A_1=\angle CC_1B_1=\angle A_1AC$,
- $\angle BAA_1=\angle C_1B_1B=\angle A_1B_1B=\angle C_1CB$,
- $\angle ABB_1=\angle C_1A_1A=\angle AA_1B_1=\angle ACC_1$.
Доказательство
Рассмотрим треугольник $ABC$, в котором проведены высоты $AA_1, BB_1, CC_1$, а точка $H$ является ортоцентром.
Заметим, что $\angle AC_1B_1=\angle BC_1A_1=\angle C$.
Тогда, так как $\angle CC_1A=90^\circ$, то $\angle CC_1B_1=90^\circ-\angle C=\angle A_1C_1C$.
C другой стороны, из прямоугольного треугольника $AA_1C$ получаем, что $\angle A_1AC=90^\circ-\angle C$.
Значит, $\angle A_1AC=\angle CC_1B_1=\angle CC_1A_1$.
Аналогично можно получить и остальные соотношения.
Следствие
Высоты треугольника являются биссектрисами его ортотреугольника (следовательно, ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).
Теорема
Пусть $AA_1, BB_1$ и $CC_1$ – высоты треугольнике $ABC$, а $H$ – ортоцентр этого треугольника. Тогда
- $\triangle ABC \sim\triangle AC_1B_1\sim\triangle BC_1A_1\sim\triangle CB_1A_1$.
- $\triangle BCH \sim\triangle B_1C_1H$
- $\triangle ABH\sim\triangle A_1B_1H$
- $\triangle ACH\sim\triangle A_1C_1H$
- $\triangle BC_1H \sim\triangle B_1CH\sim\triangle BAB_1\sim\triangle CC_1A$
- $\triangle BA_1H\sim\triangle AB_1H\sim\triangle BB_1C\sim\triangle AA_1C$
- $\triangle AC_1H\sim\triangle A_1HC\sim\triangle ABA_1\sim\triangle CC_1B$
Доказательство
С учётом первого признака подобия треугольников первый пункт теоремы напрямую следует из теоремы \ref{108b}, а второй пункт теоремы напрямую следует из теоремы \ref{108c}.
В третьем пункте теоремы $\triangle BCH\sim\triangle B_1CH$ по второму признаку подобия, так как $\angle HBC_1=\angle B_1CH$ по теореме \ref{108a}, а $\angle C_1HB=\angle B_1HC$, как вертикальные.
Подобие прямоугольных треугольников $BC_1H$ и $ABB_1$ следует из того, что острый угол $ABB_1$ для этих треугольников является общим.
Остальные подобия доказываются аналогично.
Теорема
Доказательство
Первый случай: остроугольный треугольник
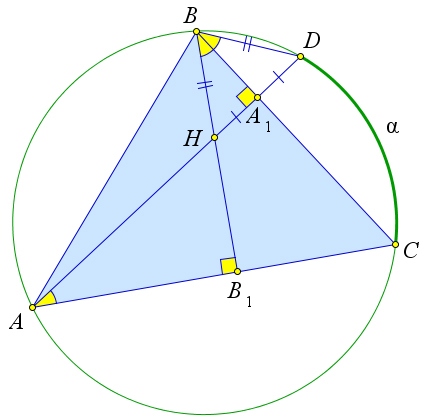
Рассмотрим треугольник $ABC$, в котором высоты $BB_1$ и $AA_1$ пересекаются в точке $H$.
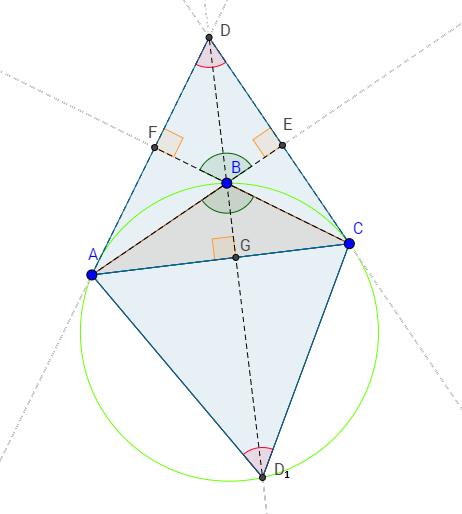
Пусть прямая $AA_1$ пересекает окружность, описанную около треугольника $ABC$, в точке $D$.
Докажем, что точка $D$ симметрична точке $H$ относительно стороны $BC$.
Так как $HD\perp BC$, то достаточно доказать, что $HA_1=A_1D$.
Пусть $\buildrel\,\,\frown\over{DC}=\alpha$.
Тогда $\angle DAC=\angle DBC=\frac{\alpha}{2}$, так как это вписанные углы.
Кроме того, так как в прямоугольных треугольниках $AHB_1$ и $BHA_1$ острые углы $\angle AHB_1$ и $\angle BHA_1$ равны, то другие острые углы тоже равны, то есть $\angle HAC=\angle HBC=\frac{\alpha}{2}$.
Тогда в треугольнике $HBD$ отрезок $BA_1$ является биссектрисой и высотой, значит, $\triangle BHD$ – равнобедренный, а $BA_1$ не только высота и биссектриса, но и медиана, то есть $HA_1=A_1D$.
Второй случай: тупоугольный треугольник
Рассмотрим треугольник $ABC$, в котором высоты $AE, BG, CF$ пересекаются в точке $D$.
Докажем, что точка $D_1$, симметричная точке $D$ относительно точки $G$ стороны $AC$, лежит на окружности, описанной около треугольника $ABC$.
Найдем чему равен $\angle AD_1C$.
Пусть $\angle ABC= α $ , тогда $\angle EBC= α$, так как они вертикальны. $\angle EDF= 180^\circ - α$ следует из того, что сумма углов в четырехугольнике равна $360^\circ$, а $\angle DEB= \angle DFB = 90^\circ$.
Треугольники $ADC$ и $AD_1C$ равны, так как каждый из которых состоит из двух треугольников, которое в свою очередь равны соответствующему треугольнику по двум сторонам и углу ($\angle G= 90^\circ, DG= D_1G$, $AC$ - общая). Из этого следует, что $\angle ADC= \angle AD_1C = 180^\circ - α$.
Предположим противное, что точка $D_1$ не лежит на окружности. Тогда существует точка $D_2$, которая лежит на окружности и на продолжении $DG$.
Докажем, что $\angle AD_2C =180^\circ - α$. $\angle B =α$ и опирается на дугу $AD_2C$. Эта дуга равна $2α$. Тогда дуга $ABC= 360^\circ -2α$, и из того, что $\angle AD_2C$ опирается на дугу $ABC$, следует: $\angle AD_2C= 180^\circ -α$.
Есть два варианта расположения точки $D_1$. Либо внутри окружности, либо за ее пределами.
Если точка $D_1$ находится внутри окружности, то получается, что $\angle D_1=\angle D_2 = α = α- \angle D_1AD_2 -\angle D_1CD_2$, где $\angle D_1AD_2≠0 $ и $\angle D_1CD_2≠0$. Такого не возможно, противоречие.
Если точка $D_1$ находится за пределами окружности, то получается, что $\angle D_1=\angle D_2 = α = α + \angle D_1AD_2 + \angle D_1CD_2$, где $\angle D_1AD_2≠0 $ и $\angle D_1CD_2≠0$. Такого тоже не возможно, противоречие.
Из противоречия следует, что точка $D_2$ равна точке $D_1$, то есть точка $D_1$ лежит на окружности.
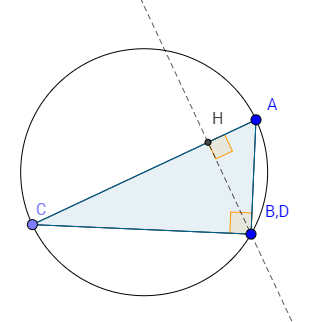
Третий случай:прямоугольный треугольник
Рассмотрим треугольник $ABC$. Его высоты пересекаются в точке $B$.
То есть точка $D$, симметричная точке $B$ относительно точки $B$ стороны $AC$, это и есть точка $B$, которая в любом случае лежит на около описанной окружности.
Теорема
Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
Доказательство
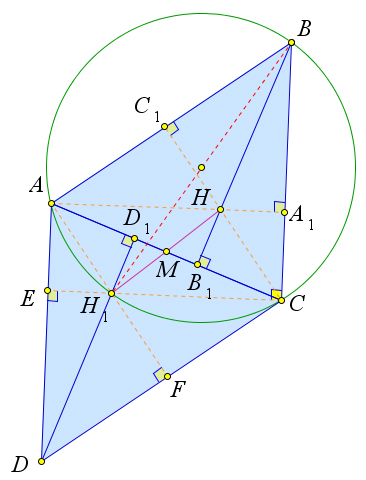
Рассмотрим треугольник $ABC$, в котором высоты $AA_1, BB_1, CC_1$ пересекаются в точке $H$.
Докажем, что точка $H_1$, симметричная точке $H$ относительно середины $M$ стороны $AC$, лежит на окружности, описанной около треугольника $ABC$, при этом $H_1B$ – это диаметр.
Рассмотрим центральную симметрию треугольника $ABC$ относительно точки $M$.
Пусть точка $D$ – это образ точки $B$ при такой симметрии, тогда треугольник $ABC$ отображается в треугольник $CAD$, а точка $H$, ортоцентр треугольника $ABC$, отображается в точку $H_1$, ортоцентр треугольника $CAD$.
Нужно доказать, что точка $H_1$ лежит на окружности, описанной около треугольника $ABC$.
Углы $B$ и $D$ равны (так как симметричные треугольники $ABC$ и $CAD$ равны).
Кроме того, так как в четырёхугольнике $DEH_1F$ углы $E$ и $А$ прямые, то $\angle AH_1F=180^\circ-\angle D=180^\circ-\angle B$.
Таким образом $\angle AH_1C+\angle B=180^\circ$.
Таким образом в четрёхугольнике $ABCH_1$ сумма противоположных углов равна $180^\circ$, а значит, он является вписанным, то есть точка $H_1$ лежит на окружности.
Докажем, что $H_1B$ – диаметр.
Так как треугольник $ABC$ отображается в треугольник $CAD$, то $\angle EAC=\angle ACB$.
Но из прямоугольного треугольника $ACE$ имеем $\angle EAC+\angle ACE=90^\circ$. Тогда $\angle ACB+\angle ACE=\angle H_1CB=90^\circ$.
А так как вписанный прямой угол опирается на диаметр, то $H_1B$ – это диаметр.
Теорема
Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
Доказательство
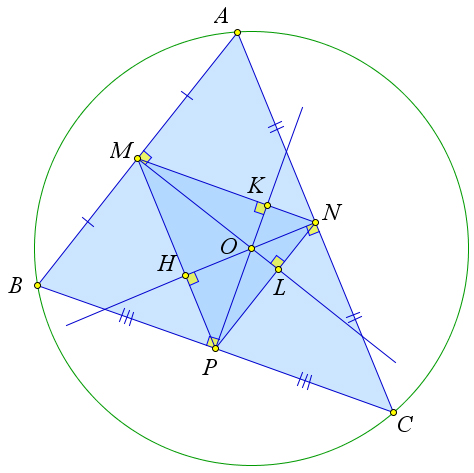
Рассмотрим треугольник $ABC$, в котором точки $M, N, P$ – это середины сторон $AB, AC, BC$, а точка $O$ – центр описанной окружности.
Докажем, что $O$ – ортоцентр треугольника $MNP$.
Так как центр описанной окружности лежит на серединных перпендикулярах к сторонам треугольника, то, например, $PO\perp BC$.
А так как $MN$ средняя линия, и, следовательно, $MN\parallel BC$, то $PO\perp MN$.
Таким образом $PK$ – это высота треугольника $MNP$.
Аналогично $ML$ и $NH$ – высоты треугольника $MNP$.
Таким образом точка $O$ является ортоцентром треугольника $MNP$.
Следствие
Точки $Z$, $O$ и $H$ лежат на одной прямой, причем $H_{Z}^{-0,5}(H)=O$, в частности, $\overrightarrow{ZH} = -2\cdot\overrightarrow{ZO}$.
Теорема
Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
Доказательство
Рассмотрим треугольник $ABC$, в котором точка $H$ – это ортоцентр, а точка $O$ – это центр описанной окружности.
Докажем, что расстояние от точки $O$ до стороны $BA$ (обозначим его $BD$) вдвое меньше отрезка $CH$.
Основываясь на следствии \ref{sle96-1}, построим треугольник $MNP$, для которого треугольник $ABC$ будет серединным.
Тогда по следствию \ref{sle96-2} точка $H$ является центром окружности, описанной около $\tri MNP$.
Таким образом отрезок $CH$ в треугольнике $MNP$ соответствует отрезку $OD$ в треугольнике $ABC$.
А так как по следствию \ref{sle96-1} эти треугольники подобны с коэффициентом $2$, получаем, что $CH=2OD$.
Теорема
Если $O$ - центр описанной окружности $\triangle ABC$, то $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$.
Доказательство
Рассмотрим треугольник $ABC$, в котором точка $O$ – центр описанной окружности, точка $H$ – ортоцентр, $D$ – середина стороны $AC$, $BB_1$ – высота.
Отложим на серединном перпендикуляре $OD$ точку $E$ так, чтобы $DE=OD$.
Тогда $AOCE$ – параллелограмм (так как диагонали точкой пересечения делятся пополам), а, следовательно, $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OE}$.
Кроме того прямые $BH$ и $OE$ перпендикулярны стороне $BC$, следовательно $BH\parallel OE$.
Кроме того по теореме \ref{117} $BH=2OD=OE$.
Следовательно, $BOEH$ – параллелограмм, а значит $\overrightarrow{OB}+\overrightarrow{OE}=\overrightarrow{OH}$.
Таким образом $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}$.
Теорема
$OH=\sqrt{9R^2-(a^2+b^2+c^2)}$ , где $R$ – радиус описанной окружности; $a,b,c$ – длины сторон треугольника.
Доказательство
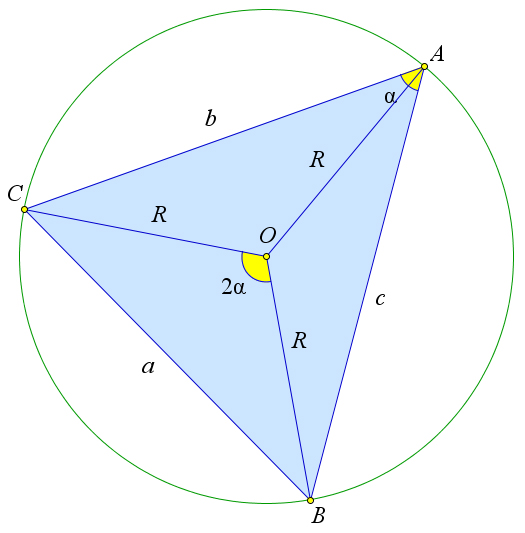
Рассмотрим остроугольный треугольник $ABC$, около которого описана окружность с центром $O$. Центральный угол $BOC$ и вписанный угол $BAC$ опираются на дугу $BC$, поэтому $\angle BAC=2\cdot\angle BOC$. Кроме того по обобщённой теореме синусов верны соотношения $a=2R\sin{A}, b=2R\sin{B}, c=2R\sin{\gamma}$. Учитывая эти соотношения, а так же теорему \ref{119}, получаем
$OH^2=\overrightarrow{OH}^2=(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})^2=$
$=OA^2+OB^2+OC^2+2\overrightarrow{OA}\cdot\overrightarrow{OB}+2\overrightarrow{OA}\cdot \overrightarrow{OC}+2\overrightarrow{OB}\cdot \overrightarrow{OC}=$
$=3R^2+2R^2\cos{2A}+2R^2\cos{2B}+2R^2\cos{2C}=$
$=3R^2+2R^2(1-2\sin^2{A})+2R^2(1-2\sin^2{B})+2R^2(1-2\sin^2{C})=$
$=9R^2-(4R^2\sin^2{A}+4R^2\sin^2{B}+4R^2\sin^2{C})=9R^2-(a^2+b^2+c^2).$
Если треугольник тупоугольный с тупым углом $\angle A$, то $\angle BAC=360^\circ-2\cdot\angle BOC$, но доказательства это не меняет, так как $ \cos{(360^\circ-2x)} = \cos{2x}$.
Если треугольник прямоугольный с прямым углом $\angle A$, то $\angle BOC = 180^\circ = 2\cdot \angle A$, и доказательство не меняется.
Следствие
$OZ = \dfrac{1}{3}\sqrt{9R^2-(a^2+b^2+c^2)}$
$ZH = \dfrac{2}{3}\sqrt{9R^2-(a^2+b^2+c^2)}$
Теорема
$HC = AB\cdot|\ctg{\gamma}|$.
Доказательство
Рассмотрим треугольник $ABC$, с высотами $BB_1$ и $CC_1$.
$HC = \dfrac{B_1C}{\sin{\alpha}}=\dfrac{BC\cdot|\cos{\gamma}|}{\sin{\alpha}} = \dfrac{AB\cdot|\cos{\gamma}|}{\sin{\gamma}} = AB\cdot|\ctg{\gamma}| $
Первое равенство следует из треугольника $B_1HC$, второе – из треугольника $BB_1C$, а третье из теоремы синусов для треугольника $ABC$. Модуль появляется из-за случая, когда $\angle С=\gamma$ – тупой.
Ссылки
https://math.stackexchange.com/questions/1767751/distance-between-incentre-and-orthocentre
$$\sqrt{2r^2-4R^2\cos A\cos B\cos C}$$
here $r$ is inradius and $R$ is circumradius. I considered $\triangle A P I(P$ is orthocentre and $I$ is incentre). I could find $A P=2 R \cos A, A I=4 R \sin \frac{B}{2} \sin \frac{C}{2}$ and $\angle P A I=\angle \frac{B-C}{2}$ So applying cosine rule I got
$\begin{align}&\small PI^2=4R^2\color{red}{\cos^2A}+16R^2\sin^2\frac{B}{2}\sin^2\frac{C}{2} -16R^2\cos A\sin\frac{B}{2}\sin\frac{C}{2}\Bigg(\cos\frac{B}{2}\cos\frac{C}{2}+\sin\frac{B}{2}\sin\frac{C}{2}\Bigg)\\&\small=4R^2\left(\cos^2A+4\sin^2\frac{B}{2}\sin^2\frac{C}{2} -4\cos A\sin\frac{B}{2}\sin\frac{C}{2}\Bigg(\cos\frac{B}{2}\cos\frac{C}{2}+\sin\frac{B}{2}\sin\frac{C}{2}\Bigg)\right)\\&\small=4R^2\left(\cos^2A+4\sin^2\frac{B}{2}\sin^2\frac{C}{2}-\cos A\cdot \color{green}{2\sin\frac{B}{2}\cos\frac{B}{2}\cdot 2\sin\frac{C}{2}\cos\frac{C}{2}}-4\cos A\sin^2\frac{B}{2}\sin^2\frac{C}{2}\right)\\&\small=4R^2\left(\cos^2A+8\sin^2\frac{B}{2}\sin^2\frac{C}{2}\cdot \color{blue}{\frac 12\left(1-\cos A\right)}-\cos A\color{green}{\sin B\sin C}\right)\\&\small=4R^2\left(\cos^2A+8\color{blue}{\sin^2\frac A2}\sin^2\frac{B}{2}\sin^2\frac{C}{2}-\cos A\sin B\sin C\right)\\&\small=4R^2\left(8\sin^2\frac A2\sin^2\frac{B}{2}\sin^2\frac{C}{2}+\cos A(\cos A-\sin B\sin C)\right)\\&\small=4R^2\left(8\sin^2\frac A2\sin^2\frac{B}{2}\sin^2\frac{C}{2}+\cos A(\cos(180^\circ-(B+C))-\sin B\sin C)\right)\\&\small=4R^2\left(8\sin^2\frac A2\sin^2\frac{B}{2}\sin^2\frac{C}{2}-\cos A\cos B\cos C\right)\\&\small =2\left(4R\sin \frac A2\sin \frac B2\sin\frac C2\right)^2-4R^2\cos A\cos B\cos C\\&\small=2r^2-4R^2\cos A\cos B\cos C\end{align}$
Теорема (расстояние между ортоцентром и инцентром)
$$HI = \sqrt{4r^2-\dfrac{a^3+b^3+c^3+abc}{2p}}.$$
Доказательство
Чтобы центр масс треугольника попал в инцентр $I$ вершины $A, B, C$ нужно загрузить массами $a, b, c$ соответственно.
Тогда для любой точки $X$ будет верно равенство $$\overrightarrow{XI} = \dfrac{a}{a+b+c}\overrightarrow{XA}+\dfrac{b}{a+b+c}\overrightarrow{XB}+\dfrac{c}{a+b+c}\overrightarrow{XC}.$$
Тогда можно взять вместо точки $X$ ортоцентр $H$:
$$\overrightarrow{HI} = \dfrac{1}{2p}\left(a\cdot \overrightarrow{HA}+b\cdot \overrightarrow{HB}+c\cdot \overrightarrow{HC}\right)$$
Вспомним, что $HA = a\ctg{\alpha}$. Тогда
$HI^2 = \dfrac{1}{4p^2}\left(a\cdot \overrightarrow{HA}+b\cdot \overrightarrow{HB}+c\cdot \overrightarrow{HC}\right)^2 = $
$ = \dfrac{1}{4p^2}\left(a^2 \overrightarrow{HA}^2+b^2 \overrightarrow{HB}^2+c^2 \overrightarrow{HC}^2+2ab\overrightarrow{HA}\cdot\overrightarrow{HB}+2bc\overrightarrow{HB}\cdot\overrightarrow{HC}+2ac\overrightarrow{HA}\cdot\overrightarrow{HC}\right)$
Лемма 0
$$\cos{\alpha}\cos{\beta}\cos{\gamma} = \dfrac{\sin^2{\alpha}+\sin^2{\beta}+\sin^2{\gamma}}{2}-1 = \dfrac{a^2+b^2+c^2}{8R^2}-1$$
Лемма 1
$a^2 \overrightarrow{HA}^2+b^2 \overrightarrow{HB}^2+c^2 \overrightarrow{HC}^2 = $
$= a^4\ctg^2{\alpha}+b^4\ctg^2{\beta}+c^4\ctg^2{\gamma} = $
$= 16R^4\sin^4{\alpha}\ctg^2{\alpha}+16R^4\sin^4{\beta}\ctg^2{\beta}+16R^4\sin^4{\gamma}\ctg^2{\gamma} = $
$= 16R^4(\sin^2{\alpha}\cos^2{\alpha}+\sin^2{\beta}\cos^2{\beta}+\sin^2{\gamma}\cos^2{\gamma}) = $
$= 16R^4(\sin^2{\alpha}-\sin^4{\alpha}+\sin^2{\beta}-\sin^4{\beta}+\sin^2{\gamma}-\sin^4{\gamma}) = $
$= 16R^4\left(\dfrac{a^2}{4R^2}+\dfrac{b^2}{4R^2}+\dfrac{c^2}{4R^2}-\dfrac{a^4}{16R^4}-\dfrac{b^4}{16R^4}-\dfrac{c^4}{16R^4}\right) = $
$=4R^2(a^2+b^2+c^2)-(a^4+b^4+c^4)$
Лемма 2
$2ab\overrightarrow{HA}\cdot\overrightarrow{HB}+2bc\overrightarrow{HB}\cdot\overrightarrow{HC}+2ac\overrightarrow{HA}\cdot\overrightarrow{HC} = $
$ = +2a^2b^2\ctg^2{\alpha}\ctg^2{\beta}\cos{(180^\circ-\gamma)} + 2b^2c^2\ctg^2{\beta}\ctg^2{\gamma}\cos{(180^\circ-\alpha)} + 2a^2c^2\ctg^2{\alpha}\ctg^2{\gamma}\cos{(180^\circ-\beta)} = $
$ = -2a^2b^2\ctg^2{\alpha}\ctg^2{\beta}\cos{\gamma} - 2b^2c^2\ctg^2{\beta}\ctg^2{\gamma}\cos{\alpha} - 2a^2c^2\ctg^2{\alpha}\ctg^2{\gamma}\cos{\beta} = $
$ = -2\cos{\alpha}\cos{\beta}\cos{\gamma}\left(\dfrac{a^2b^2}{\sin{\alpha}\sin{\beta}}+\dfrac{b^2c^2}{\sin{\beta}\sin{\gamma}}+\dfrac{a^2c^2}{\sin{\alpha}\sin{\gamma}}\right) = $
$ = -2\cos{\alpha}\cos{\beta}\cos{\gamma}\left(4R^2ab+4R^2bc+4R^2ac\right) = $
$ = -2\left(\dfrac{a^2+b^2+c^2}{8R^2}-1\right)4R^2\left(ab+bc+ac\right) = $
$ = 4R^2\left(2ab+2bc+2ac\right)-(a^2+b^2+c^2)(ab+bc+ac)$
продолжение доказательства
Тогда
$HI^2 = \dfrac{1}{4p^2}\left(a^2 \overrightarrow{HA}^2+b^2 \overrightarrow{HB}^2+c^2 \overrightarrow{HC}^2+2ab\overrightarrow{HA}\cdot\overrightarrow{HB}+2bc\overrightarrow{HB}\cdot\overrightarrow{HC}+2ac\overrightarrow{HA}\cdot\overrightarrow{HC}\right)$
$= \dfrac{1}{4p^2}\left(4R^2(a^2+b^2+c^2)-(a^4+b^4+c^4)+4R^2\left(2ab+2bc+2ac\right)-(a^2+b^2+c^2)(ab+bc+ac)\right) = $
$= \dfrac{1}{4p^2}\left(4R^2(a^2+b^2+c^2+2ab+2bc+2ac)-(a^4+b^4+c^4+(a^2+b^2+c^2)(ab+bc+ac))\right) = $
$= \dfrac{1}{4p^2}\left(4R^2(a+b+c)^2-(a^4+b^4+c^4+a^3b+a^2bc+a^3c+ab^3+b^3c+b^2ac+abc^2+bc^3+ac^3)\right) = $
$= \dfrac{1}{4p^2}\left(16R^2p^2-(a^4+a^3b+a^3c+ab^3+b^4+cb^3+ac^3+bc^3+c^4+a^2bc+ab^2c+abc^2)\right)=$
$= \dfrac{1}{4p^2}\left(16R^2p^2-(a^3(a+b+c)+b^3(a+b+c)+c^3(a+b+c)+abc(a+b+c))\right) =$
$= \dfrac{1}{4p^2}\left(16R^2p^2-(a^3+b^3+c^3+abc)2p\right) =$
$= 4R^2-\dfrac{a^3+b^3+c^3+abc}{a+b+c}$