Президентский ФМЛ №239

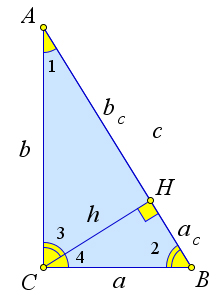
Пусть в прямоугольном треугольнике $ABC$ из вершины прямого угла $C$ проведена высота $CH$, $AB=c, BC=a, CA=b, AH=b_c, BH=a_c$. В этих обозначениях выполняются следующие соотношения:

1. $h=\sqrt{a_cb_c}$.
2. $h=\frac{ab}{c}$.
3. $\dfrac{a_c}{b_c}=\dfrac{a^2}{b^2}$.
4. $a^2=a_cc$.

Докажем, что треугольники $ABC$, $ACH$ и $CHB$ подобны.

Из треугольника $ABC$ $\angle 2=90^\circ-\angle 1$. C другой стороны из треугольника $CHA$ $\angle 3=90^\circ-\angle 1$, следовательно $\angle 2=\angle 3$. Кроме того $\angle 4=90^\circ-\angle 3=\angle 1$.

Следовательно, треугольники $ABC$, $ACH$ и $CHB$ подобны по первому признаку подобия треугольников.

Тогда из подобия треугольников $ABC$ и $ACH$ получаем: $\dfrac{h}{a}=\dfrac{b}{c}=\dfrac{b_c}{b}$.

Откуда получаем, что $h=\dfrac{ab}{c}$.

Из подобия треугольник $ACH$ и $BCH$ получаем: $\dfrac{b}{a}=\dfrac{b_c}{h}=\dfrac{h}{a_c}$.

Откуда получаем, что $h^2=a_cb_c$ и $b_c=\dfrac{hb}{a}$.

Из подобия треугольников $BCH$ и $ABC$ получаем: $\dfrac{a}{c}=\dfrac{a_c}{a}=\dfrac{h}{b}$.

Кроме того $a_c=\dfrac{ha}{b}$.

Разделив эту формулу на формулу для $b_c$, полученную из второй пропорции, получим $\dfrac{a_c}{b_c}=\dfrac{a^2}{b^2}$.

Кроме того из пропорции $\dfrac{a}{c}=\dfrac{a_c}{a}$ получим, $a^2=a_c\cdot c$.