Это старая версия документа!
Теорема
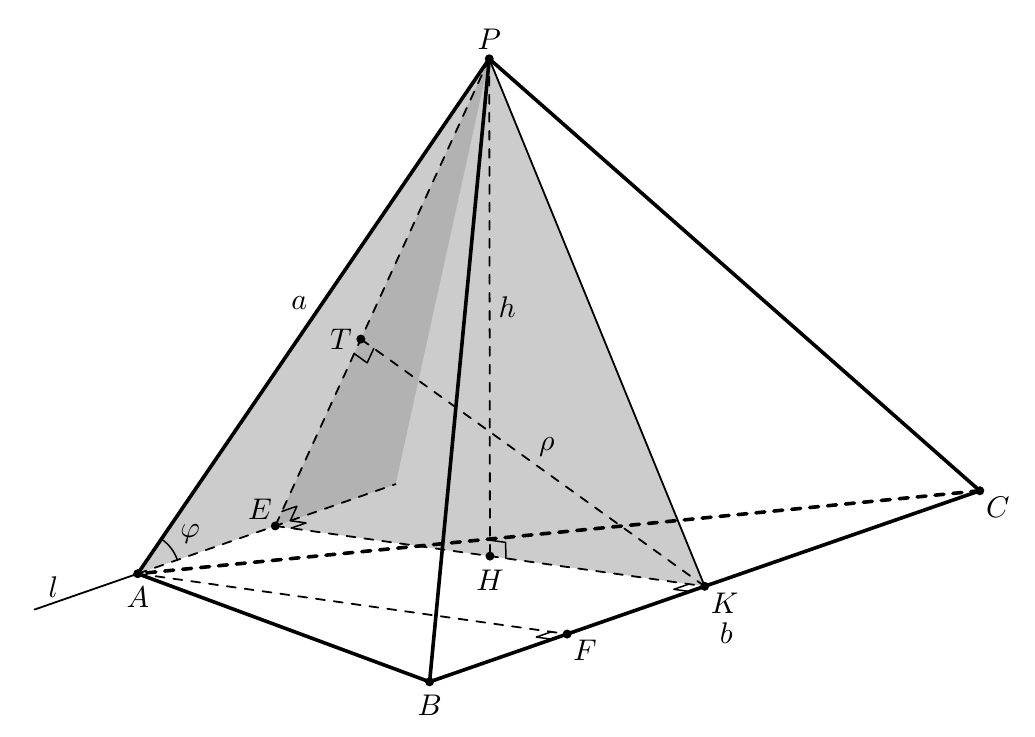
Пусть в тетраэдре $PABC$ известно, что $PA=a, BC=b, \angle(AP,BC)=\varphi$.
Тогда расстояние $\rho$ между ребрами $AP$ и $BC$ вычисляется из соотношения $$V = \dfrac{1}{6}\cdot\rho\cdot a\cdot b\cdot \sin{\varphi},$$ где $V=\dfrac{1}{3}\cdot h\cdot S$ — то есть треть произведения любой высоты тетраэдра на площадь грани, к которой эта высота проведена.
Доказательство:
Проведем через вершину $A$ прямую $l$, параллельную прямой $BC$, и опустим на нее перпендикуляр $PE$ из точки $P$. Таким образом, получим, что $AE\parallel BC$, а значит $\angle PAE = \angle(AP, BC) = \varphi$.
Из прямоугольного треугольника $PAE$ получаем: $PE = a \cdot \sin{\varphi}$.
Проведем из точки $E$ перпендикуляр $EK$ к прямой $BC$ в плоскости $ABC$.
$EK$ равно высоте треугольника $ABC$, проведенной из точки $A$, то есть $EK = AF$.
Поскольку $PAE\parallel BC$, то расстояние от прямой $BC$ до прямой $AP$ равно расстоянию то точки $K$ до плоскости $PAE$.
Поскольку $PE\perp AE$ и $EK\perp AE$, то по теореме о трех перпендикулярах перпендикуляр $KT$ из точки $K$ к плоскости $PAE$ падает на прямую $PE$, а высота $PH$ из точки $P$ на плоскость $ABC$ падает на прямую $EK$.
Выпишем площадь треугольника $PEK$ двумя способами: $S(PEK) = 0,5\cdot PH\cdot EK = 0,5\cdot KT\cdot PE$.
Тогда $\rho = KT = \dfrac{PH\cdot EK}{PE} = \dfrac{PH\cdot AF}{a\cdot\sin{\varphi}} = \dfrac{PH\cdot AF\cdot BC}{a\cdot\sin{\varphi}\cdot BC}=\dfrac{PH\cdot 2\cdot S(ABC)}{a\cdot b\cdot\sin{\varphi}}$.
Итак, $\rho = \dfrac{2\cdot PH\cdot S(ABC)}{a\cdot b\cdot\sin{\varphi}}$.
Обратим внимание, что тогда $PH\cdot S(ABC) = \dfrac{1}{2}\rho\cdot a\cdot b\cdot \sin{\varphi}$. В левой части этого равенства стоит произведение высоты тетраэдра на площадь грани, к которой эта высота проведена.
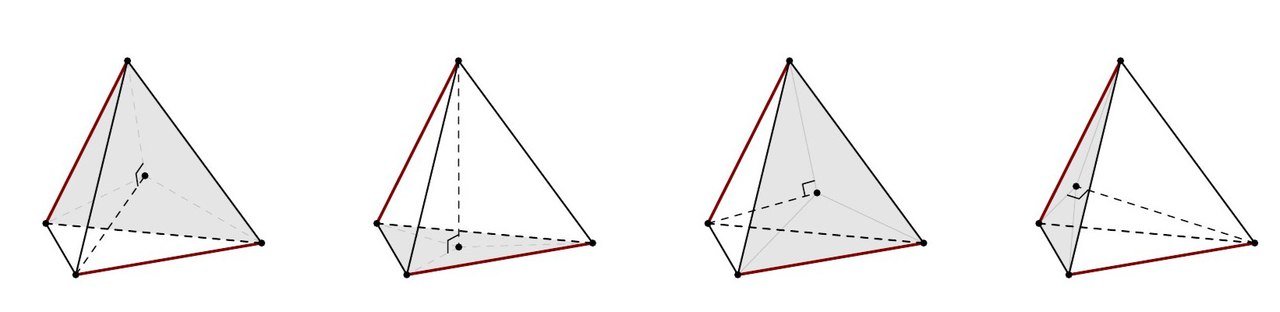
Но несложно видеть (см. рисунок), что можно выбрать другую высоту и площадь другого треугольника, и результат получится аналогичный. Например, можно мысленно все тетраэдры на рисунке поставить на закрашенную грань и повернуть вокруг вертикальной оси так, чтобы расположение красных ребер, высоты и закрашенной грани стало одинаковым.
А поскольку произведение $\dfrac{1}{2}\rho\cdot a\cdot b\cdot \sin{\varphi}$ не зависит от выбора высоты и грани, то произведение высоты тетраэдра на площадь грани, к которой эта высота проведена, является постоянной величиной для данного тетраэдра.
Обозначим $V = \dfrac{1}{3} \cdot PH \cdot S(ABC)$.
Тогда формула примет вид: $V = \dfrac{1}{6}\cdot\rho\cdot a\cdot b\cdot \sin{\varphi}$.