Это старая версия документа!
Содержание
Назад — Оглавление — Вперед
Многоугольники.
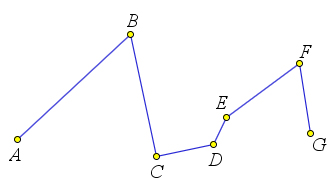
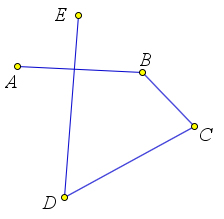
Ломаная
Определение
Ломаной линией, или короче, ломаной, называется конечная последовательность отрезков, такая, что один из концов первого отрезка служит концом второго, другой конец второго отрезка служит концом третьего и т.д. При этом соседние отрезки не лежат на одной прямой. Эти отрезки называют звеньями ломаной.
Виды ломаной
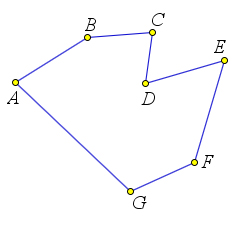
- Ломаная называется замкнутой, если начало первого отрезка совпадает с концом последнего.
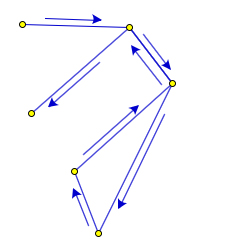
- Ломаная может пересекать сама себя, коснуться сама себя, налегать на себя. Если таких особенностей нет, то такая ломаная называется простой.
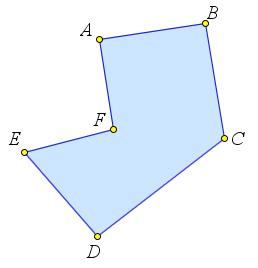
Многоугольники
Определение
Замечание
В каждой вершине многоугольника его стороны задают некоторый угол многоугольника. Он может быть как меньше развернутого, так и больше развернутого.
Свойство
У каждого многоугольника есть угол, меньший $180^\circ$.
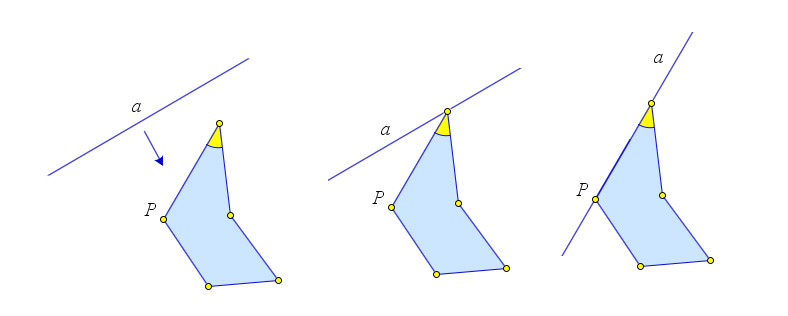
Доказательство
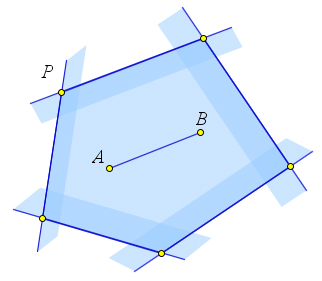
Пусть дан многоугольник $P$.
Проведем какую-нибудь прямую, не пересекающую его. Будем перемещать ее параллельно в сторону многоугольника. В некоторый момент мы впервые получим прямую $a$, имеющую с многоугольником $P$ хотя бы одну общую точку. От этой прямой многоугольник лежит по одну сторону (при этом некоторые его точки лежат на прямой $a$).
На прямой $a$ лежит хотя бы одна вершина многоугольника. В ней сходится две его стороны, расположенные по одну сторону от прямой $a$ (считая и тот случай, когда одна из них лежит на этой прямой). А значит, при этой вершине угол меньше развернутого.
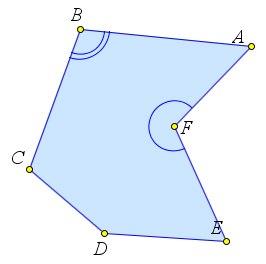
Определение
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Если многоугольник не является выпуклым, его называют невыпуклым.
Замечание
Выпуклый многоугольник является пересечением полуплоскостей, ограниченных прямыми, которые содержат стороны многоугольника.
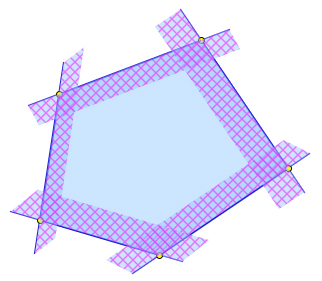
Свойства выпуклого многоугольника
- У выпуклого многоугольника все углы меньше $180^\circ$.
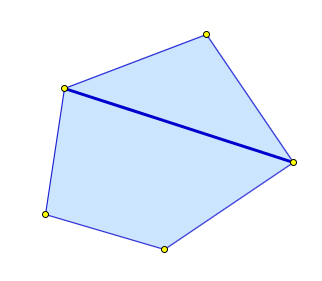
- Отрезок, соединяющий любые две точки выпуклого многоугольника (в частности, любая его диагональ), содержится в этом многоугольнике.
Доказательство
Докажем первое свойство
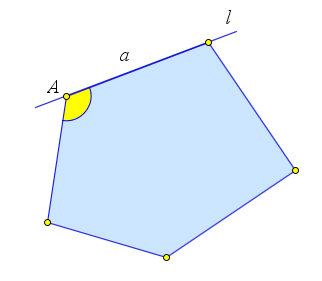
Возьмем любой угол $A$ выпуклого многоугольника $P$ и его сторону $a$, идущую из вершины $A$. Пусть $l$ – прямая, содержащая сторону $a$. Так как многоугольник $P$ выпуклый, то он лежит по одну сторону от прямой $l$. Следовательно, и его угол $A$ лежит по одну сторону от этой прямой. Значит угол $A$ меньше развернутого угла, то есть меньше $180^\circ$.
Докажем второе свойство
Возьмем любые две точки $A$ и $B$ выпуклого многоугольника $P$. Многоугольник $P$ является пересечением нескольких полуплоскостей. Отрезок $AB$ содержится в каждой из этих полуплоскостей. Поэтому он содержится и в многоугольнике $P$.
Определение
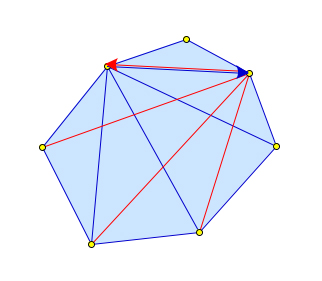
Теорема (о количестве диагоналей n-угольника)
Количество диагоналей выпуклого $n$-угольника вычисляется по формуле $\dfrac{n(n-3)}{2}$.
Доказательство
Из каждой вершины n-угольника можно провести $n-3$ диагонали (нельзя провести диагональ в соседние вершины и в саму эту вершину). Если посчитать все такие возможные отрезки, то их будет $n\cdot(n-3)$, так как вершин $n$. Но каждая диагональ будет посчитана дважды. Таким образом, количество диагоналей n-угольника равно $\dfrac{n(n-3)}{2}$.
Теорема (о сумме углов n-угольника)
Доказательство
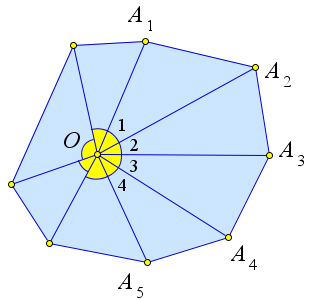
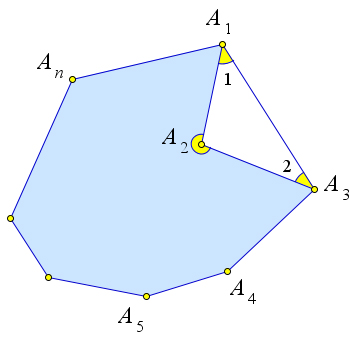
Рассмотрим $n$-угольник $A_1A_2A_3\ldots A_n$.
Возьмём внутри этого многоугольника произвольную точку $O$.
Сумма углов всех треугольников $A_1OA_2$, $A_2OA_3$, $A_3OA_4$, $\ldots$, $A_{n-1}OA_n$ равна $180^\circ\cdot n$.
C другой стороны эта сумма складывается из суммы всех внутренних углов многоугольника и полного угла $\angle O=\angle 1+\angle 2+\angle 3+\ldots=30^\circ$.
Тогда сумма углов рассматриваемого $n$-угольника равна $180^\circ\cdot n-360^\circ=180^\circ\cdot(n-2)$.
Теорема
Теорема (о сумме внешних углов выпуклого n-угольника)
Доказательство
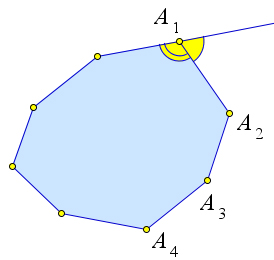
Внешний угол при вершине $A_1$ равен $180^\circ-\angle A_1$.
Сумма всех внешних углов равна:
$\sum\limits_{n}(180^\circ-\angle A_n)=n\cdot180^\circ - \sum\limits_{n}A_n=n\cdot180^\circ - 180^\circ\cdot(n-2)=360^\circ$.