1. Против большей стороны треугольника лежит больший угол.
2. Против большего угла треугольника лежит большая сторона.

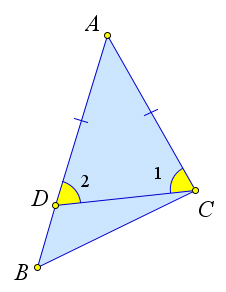
Рассмотрим произвольный треугольник $ABC$.

Пусть $AB>AC$.

Докажем, что $\angle C>\angle B$.

Отложим на стороне $AB$ отрезок $AD$, равный стороне $AC$.

Так как $AD

Следовательно, угол $\angle 1$ является частью угла $C$ и, значит, $\angle C<\angle 1$.

Угол $\angle 2$ – внешний угол треугольника $BDC$, поэтому $\angle 2>\angle B$.

Углы $\angle 1$ и $\angle 2$ равны, как углы при основании равнобедренного треугольника $ADC$.

Таким образом, $\angle C>\angle 1=\angle 2>\angle B$.

Пусть в треугольнике $ABC$ $\angle C>\angle B$.

Докажем, что $AB>AC$.

Предположим противное.

Тогда либо $AB=AC$, либо $AB

В первом случае треугольник $ABC$ – равнобедренный и, значит, $\angle C=\angle B$.

Во втором случае $\angle B>\angle C$ (против большей стороны лежит больший угол).

И то, и другое противоречит условию $\angle C>\angle B$.

Поэтому предположение неверно, и, следовательно, $AB>AC$.

Гипотенуза прямоугольного треугольника больше катета.

Если из одной точки проведены к прямой перпендикуляр и наклонные, то перпендикуляр короче наклонных, а большей наклонной соответствует большая проекция и наоборот.

Каждая сторона треугольника меньше суммы двух других сторон.

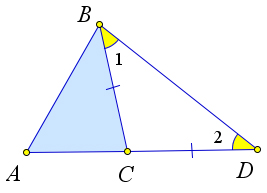
Рассмотрим треугольник $ABC$ и докажем, что $AB

Отложим на продолжении стороны $AC$ отрезок $CD$, равный стороне $CB$.

В равнобедренном треугольнике $BCD$ $\angle 1=\angle 2$, а в треугольнике $ABD$ $\angle ABD>\angle 1$ и, значит, $\angle ABD>\angle 2$.

Тогда по теореме $AB

По теореме косинусов $AB=\sqrt{AC^2+CB^2-2\cdot AB \cdot AC\cdot \cos{\hat{C}}}<\sqrt{AC^2+CB^2+2\cdot AB \cdot AC}=|AC + CB|<|AC|+|CB|=AC+CB$.

Здесь в первом неравенстве использовали то, что $\cos{\hat{C}}\geq-1$, а в последнем неравенстве использовали алгебраическое свойства модуля: $|a+b|<|a|+|b|$.