Содержание
Теорема
Если $CC_1$ – биссектриса треугольника $ABC$, то $CC_1=\sqrt{AC\cdot CB-AC_1\cdot C_1B}$.
Доказательство
Первый способ
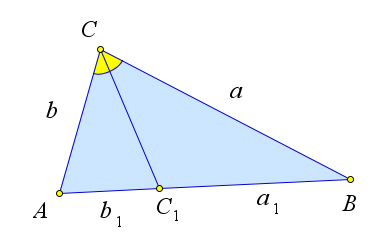
Рассмотрим треугольник $ABC$, в котором проведена биссектриса $CC_1$.
Пусть $AC=b, BC=a, AC_1=b_1, BC_1=a_1, CC_1=l$.
Докажем, что $l=\sqrt{ab-a_1b_1}$.
Рассмотрим случай, когда $a=b$, то есть треугольник $ABC$ – равнобедренный.
Тогда $CC_1$ – биссектриса и высота, и требуемая формула обращается в теорему Пифагора для треугольника $ACC_1$: $l=\sqrt{b^2-b_1^2}$.
Рассмотрим случай, когда $a\neq b$.
Обозначим половину угла $C$ за $\alpha$, и выразим $\cos{\alpha}$ по теореме косинусов двумя способам: из треугольников $ACC_1$ и $BCC_1$.
Получим $\cos{\alpha}=\dfrac{a^2+l^2-a_1^2}{2al}=\dfrac{b^2+l^2-b_1^2}{2bl}$.
Откуда $a^2b+l^2b-a_1^2b=b^2a+l^2a-b_1^2a$.
Тогда $l^2(b-a)=ab(b-a)+a_1^2b-b_1^2a=ab(b-a)+a_1\cdot a_1b-b_1\cdot b_1a$.
По свойству биссектрисы $\dfrac{a}{b}=\dfrac{a_1}{b_1}$ или $ab_1=ba_1$.
Следовательно, $l^2(b-a)=ab(b-a)+a_1\cdot b_1a-b_1\cdot a_1b=ab(b-a)-a_1b_1(b-a)$.
И поскольку треугольник $a\neq b$, то $l^2=ab-a_1b_1$ или $l=\sqrt{ab-a_1b_1}$.
Второй способ
Рассмотрим треугольник $ABC$, в котором проведена биссектриса $CC_1$.
Пусть $AC=b, BC=a, AC_1=b_1, BC_1=a_1, CC_1=l$.
Докажем, что $l=\sqrt{ab-a_1b_1}$.
По свойству биссектрисы $AC_1:C_1B=b:a$, тогда $BC_1=\dfrac{ca}{a+b}$, $AC_1=\dfrac{cb}{a+b}$.
По теореме косинусов для треугольника $ABC$: $\cos{B}=\dfrac{a^2+c^2-b^2}{2ac}$.
По теореме косинусов для треугольника $BCC_1$:
$l^2=a^2+BC_1^2-2\cdot a\cdot BC_1\cdot \cos{B}= a^2+\left(\dfrac{ca}{a+b}\right)^2-2\cdot a\cdot \dfrac{ac}{a+b}\cdot\dfrac{a^2+c^2-b^2}{2ac} = a^2+\dfrac{c^2a^2}{(a+b)^2}-\dfrac{(a^3+ac^2-ab^2)(a+b)}{(a+b)^2}=\dfrac{a^2(a^2+b^2+2ab)+a^2c^2-a^4-a^2c^2+a^2b^2-a^3b-abc^2+ab^3}{(a+b)^2}=\dfrac{a^3b+2a^2b^2+ab^3-abc^2}{(a+b)^2}=\dfrac{ab(a+b)^2-abc^2}{(a+b)^2}=ab-\dfrac{ac}{a+b}\cdot\dfrac{bc}{a+b}=ab-a_1b_1$.
Таким образом $l=\sqrt{ab-a_1b_1}$.
Теорема
Если $CC_1$ – биссектриса треугольника $ABC$, то $CC_1^2=a\cdot b-a_1\cdot b_1$.
Доказательство
Опишем окружность вокруг треугольника $ABC$.
Продлим биссектрису $l_c$ до пересечения с окружностью в точке $D$
$\triangle ABD\sim\triangle OBC$, так как $\angle ABD=\angle DBC$ и $\angle OCB=\angle ADB$
$\dfrac{l_c + x}{b}=\dfrac{a}{l_c}$.
$l_c(l_c+x)=ab$.
$l_c^2 + l_cx=ab$.
$l_cx=a_1b_1$. (по теореме об отрезках хорд)
$l_c^2=a\cdot b-a_1\cdot b_1$.
Теорема
Если $l_c$ – биссектриса треугольника $ABC$, проведенная из вершины $C$, то
- $l_c = \dfrac{2ab\cos{\dfrac{\gamma}{2}}}{a+b}$.
- $l_c = \dfrac{2\sqrt{abp(p-c)}}{a+b}$.
- $l_c = \dfrac{2\sqrt{ab(a+b+c)(a+b-c)}}{a+b}$.