1. Окружность – это геометрическое место точек, равноудаленных от данной точки.

2. Геометрическое место точек, удаленных от заданной точки $O$ на заданное расстояние $R$, называют окружностью с центром в точке $O$ и радиусом $R$.

Обозначают такую окружность так: $\omega(O;R)$.

Если $d$ – это расстояние от точки $O$ до прямой $l$, а $\omega$ – окружность с центром в точке $O$ и радиусом $R$, тогда

1. если $d>R$, то прямая не пересекает окружность;
2. если $d=R$, то прямая является касательной к окружности;
3. если $d<R$, то прямая пересекает окружность в двух точках.

Пусть $d

На прямой $p$ от точки $H$ отложим два отрезка $HA$ и $HB$, длины которых равны $\sqrt{r^2-d^2}$.

По теореме Пифагора $OA=OB=\sqrt{OH^2+HA^2}=\sqrt{d^2+(r^2-d^2)}=r$.

Следовательно, точки $A$ и $B$ лежат на окружности и, значит, являются общими точками прямой $p$ и данной окружности.

Докажем, что прямая $p$ и данная окружность не имеют других общих точек.

Предположим, что они имеют ещё одну общую точку $C$.

Тогда медиана $OD$ равнобедренного треугольника $OAC$, проведенная к основанию $AC$, является высотой этого треугольника, поэтому $OD\perp p$.

Отрезки $OD$ и $OH$ не совпадают, так как середина $D$ отрезка $AC$ не совпадает с точкой $H$ – серединой отрезка $AB$.

Получается, что из точки $O$ проведены два перпендикуляра: отрезки $OH$ и $OD$ – к прямой $p$, что невозможно.

Пусть $d=r$.

В этом случае $OH=r$, то есть точка $H$ лежит на окружности и, значит, является общей точкой прямой и окружности.

Прямая $p$ и окружность не имеют других общих точек, так как для любой точки $M$ прямой $p$, отличной от точки $H$, $OM>OH=r$ (наклонная $OM$ больше перпендикуляра $OH$), и, следовательно, точка $M$ не лежит на окружности.

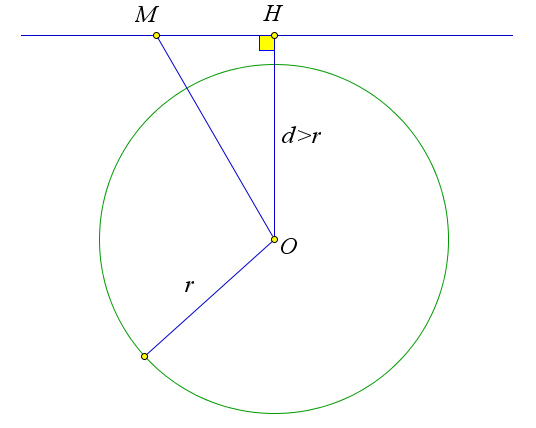
Пусть $d>r$.

В этом случае $OH>r$, поэтому для любой точки $M$ прямой $p$ $OM\geqslant OH>r$.

Следовательно, точка $M$ не лежит на окружности.

1. Прямая, имеющая с окружностью только одну общую точку, называется касательной к этой окружности.
2. Прямая, имеющая с окружностью две общие точки, называется секущей к данной окружностью.

Касательная к кривой – это предельное положение секущей.

1. (Свойство касательной): касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. (Признак касательной): если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведенному в эту точку, то она является касательной.

Пусть $p$ – касательная к окружности с центром $O$, $A$ – точка касания.

Докажем, что $p\perp OA$.

Предположим, что это не так.

Тогда радиус $OA$ является наклонной к прямой $p$.

Так как перпендикуляр, проведенный из точки $O$ к прямой $p$, меньше наклонной $OA$, то расстояние от от точки $O$ до прямой $p$ меньше радиуса.

Следовательно, прямая $p$ и окружность имеют две общие точки.

Но это противоречит условию, так как $p$ – это касательная.

Таким образом $p\perp OA$.

Из условия следует, что данный радиус является перпендикуляром, проведенным из центра окружности к данной прямой.

Поэтому расстояние от центра окружности до прямой равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку.

Но это и означает, что данная прямая является касательной к окружности.

1. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
2. Если прямые, проходящие через точку $M$, касаются окружности в точках $A$ и $B$, то $MA=MB$.
3. Если прямые, проходящие через точку $M$, касаются окружности в точках $A$ и $B$, и $AB$ пересекает $MO$ в точке $H$, то $AB\perp MO$ и $AH=HB$

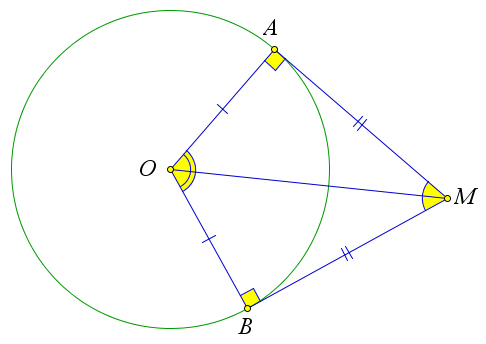
Рассмотрим окружность с центром в точке $O$, вписанную в угол $M$.

Пусть данная окружность касается сторон угла в точках $A$ и $B$.

Докажем, что $\angle AMO=\angle BMO$.

Действительно, треугольники $AMO$ и $BMO$ равны, по катету и гипотенузе ($OA=OB$, $OM$ – общая).

Тогда $\angle AMO=\angle BMO$ и $MA=MB$.

Кроме того, так как треугольник $\triangle MAB$ равнобедренный, а $MH$ – не только биссектриса угла $\angle AMB$, но и медиана и высота, то есть $AH=HB, AB\perp MO$.

1. Диаметр перпендикулярен хорде, тогда и только тогда, когда он проходит через ее середину.
2. Хорды одной окружности равны тогда и только тогда, когда они равноудалены от ее центра.
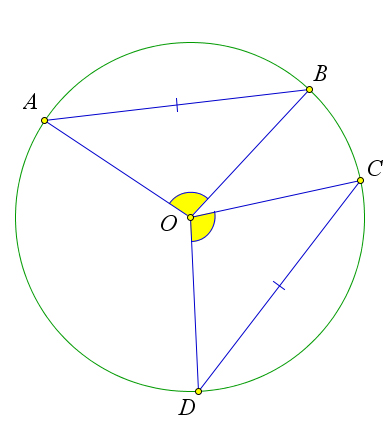
3. Хорды одной окружности равны тогда и только тогда, когда они стягивают равные центральные углы.

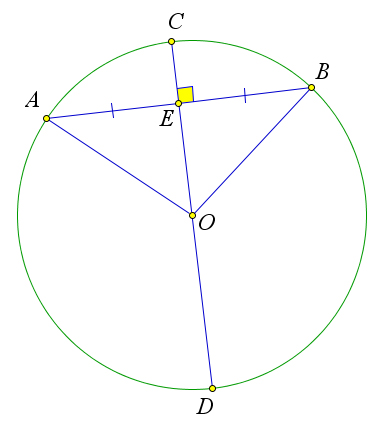
Рассмотрим окружность с центром $O$, в которой хорда $AB$ пересекает диаметр $CD$ в точке $E$.

Если $E$ – это середина $AB$, то $OE$ – это медиана равнобедренного треугольника $AOB$, а, следовательно, и $OE$ – высота.

Обратно, если $OE$ - высота, то и медиана.

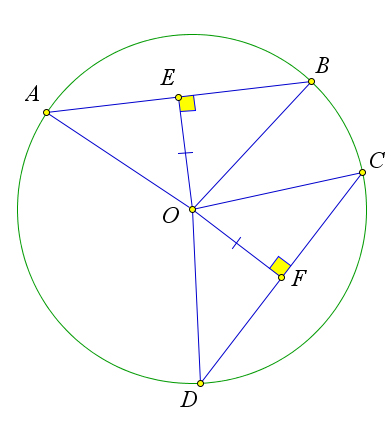
Рассмотрим окружность с центром $O$, в которой проведены хорды $AB$ и $CD$.

Пусть расстояния $OE$ и $OF$ до этих хорд равны.

Тогда треугольники $OAE, OEB, OFD$ и $OFC$ равны по катету и гипотенузе ($OA=OB=OD=OC$, так как это радиусы).

Тогда $AE=EB=DF=FC$, и, следовательно, $AB=2AE=2DF=CD$.

Рассмотрим окружность с центром $O$, в которой проведены хорды $AB$ и $CD$.

Если $\angle AOB=\angle COD$, то $\triangle AOB=\triangle COD$ по первому признаку равенства ($CO=OB=OD=OA$, так как это радиусы), следовательно, $AB=CD$.

Обратно, если $AB=CD$, то $\triangle AOB=\triangle COD$ по третьему признаку равенства, следовательно, $\angle AOB=\angle COD$.

1. Точка касания двух окружностей лежит на прямой, соединяющей их центры.
2. Центры двух пересекающихся окружностей лежат на серединном перпендикуляре к их общей хорде.

1. Если $R+r
2. Если $R+r=d$, то окружности касаются внешним образом.
3. Если $R-r
4. Если $R-r=d$, то окружности касаются внешним образом.
5. Если $R-r>d$, то окружности не пересекаются, и одна окружность лежит внутри другой.